Problem

Find the length of the median of a triangle through its sides. The sides of the triangle are 8, 9, and 13 centimeters. A median is drawn to the largest
side of the triangle. Determine the median of the triangle based on the sizes of its sides.

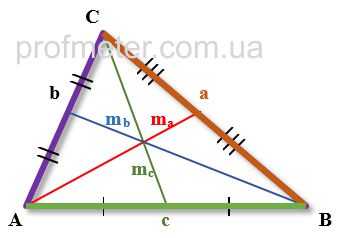
Solution

There are two methods to solve this problem.

Method 1: Using Stewart's Theorem

Stewart's Theorem states that the square of the median is equal to one fourth of the sum of the doubled squares of the sides from which the square
of the side to which the median is drawn was subtracted.

The formula for finding the length of the median m_c of a triangle through the lengths of its sides is:

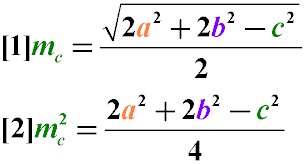
Given:

• a=8a = 8 cm
• b=9b = 9 cm
• c=13c = 13 cm (the largest side)

Substitute the values into the formula:

Method 2: Using the Parallelogram Construction

This method involves constructing a parallelogram to find the median.

1. Extend the side of the triangle ABC and the median BO by adding them to form a parallelogram.
2. The median BO of the triangle ABC will be equal to half the diagonal of the resulting parallelogram.
3. The two sides of the triangle AB and BC will be the lateral sides of the parallelogram.
4. The third side of the triangle AC, to which the median was drawn, is the second diagonal of the resulting parallelogram.

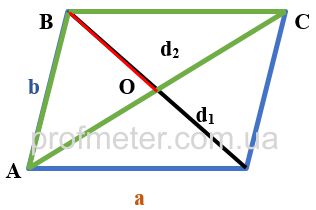
According to the theorem, the sum of the squares of the diagonals of a parallelogram is equal to twice the sum of the squares of its sides:

Let d₁ be the diagonal formed by the extension of the median of the original triangle, and d₂=13 cm (the largest side):

Since the median sought is equal to half the diagonal of the parallelogram:

Answer

The length of the median of the triangle is 5.5 cm.