How to Find the Volume of a Triangular Prism (with a Triangle at the Base)

If the base of a prism is a triangle, then to find its volume, you can use the formulas for finding the area of the triangle and multiply the resulting
value by the height of the prism.

Formulas for Finding the Volume of a Triangular Prism

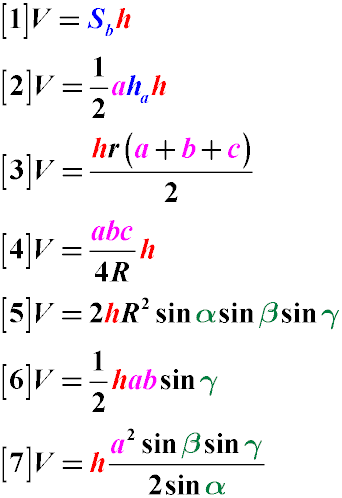
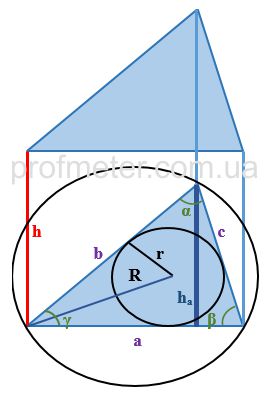
1. Volume through the Height of the Base: The volume of a triangular prism can be found through the height of the base h_a and the side a to which this
   height is dropped, where h is the height of the prism. Do not confuse h_a and h. (Formula 2)

2. Volume through the Radius of the Inscribed Circle: The volume of a triangular prism can be found through the radius of the inscribed circle r and
   the sum of the lengths of the sides of the base a, b, c (Formula 3)

3. Volume through the Radius of the Circumscribed Circle: The volume of a triangular prism can be calculated as the product of the lengths of the sides
   of the base by four times the radius of the circumscribed circle R, multiplied by the height of the prism (Formula 4)

4. Volume through the Sines of the Angles: Knowing the radius of the circumscribed circle, the volume of a triangular prism can be found as the product
   of the sines of all angles of the base by the square of the radius of the circumscribed circle, multiplied by twice the height of the prism (Formula 5)

5. Volume through the Angle between Two Sides: If the angle between two sides of the base and these sides themselves are known, then half the
   product of the sides of the base by the sine of the angle between them and by the height of the prism will also allow you to calculate its volume (Formula 6)

Special Cases

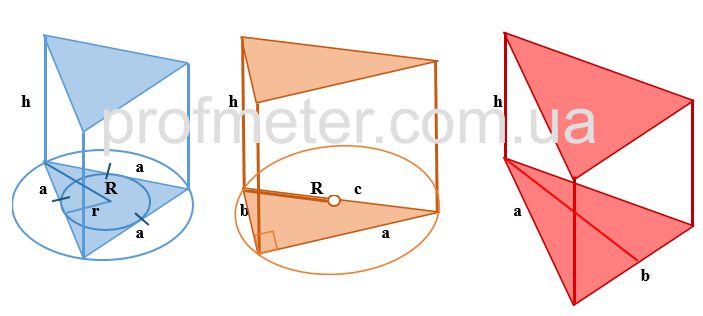
There are also formulas for finding the volume of a prism for special cases when the base is a geometric figure with "singularities". For example, if the base
of a right prism is an equilateral, rectangular, or isosceles triangle, then the number of formulas that can be used to calculate the volume of a prism is
significantly expanded.