|
Note. This is part of the lesson with geometry problems (parallelogram section). If you need to solve a geometry problem
that is not here, write about it in the forum.
See also: Properties and area of a parallelogram.
Height of a Parallelogram - Formulas and Properties
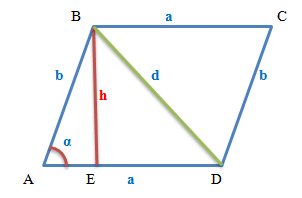
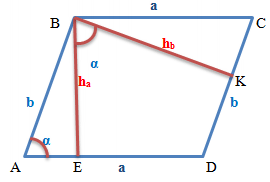
Parallelogram with Height Lowered to the Base
A parallelogram with two heights lowered to both bases and the angle between bases.
The symbols in the formulas are equivalent to the symbols in the figures, namely:
-
a: Sides of the parallelogram, parallel to each other.
-
b: Lateral sides of the parallelogram.
-
h: Height of the parallelogram.
-
d: Diagonal of the parallelogram.
-
S: Area of the parallelogram.
-
α: Acute angle at the base of the parallelogram.
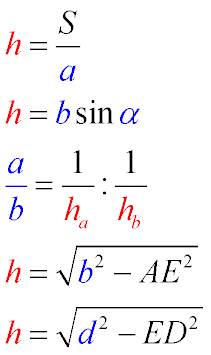
Formulas for Finding the Height of the Parallelogram Through Sides, Angles, and Diagonals
-
The height of a parallelogram is equal to the ratio of the area to the base (1)
-
The height of a parallelogram is equal to the product of the side by the sine of the angle at its base (2)
-
The ratio of the bases of a parallelogram is equal to the inversely proportional ratio of the heights dropped to
the corresponding sides (3)
-
The height of a parallelogram is equal to the square root of the difference between the square of the side and
the square of the length of the segment forming a right triangle, the other sides of which are the side and the height (4)
-
The height of a parallelogram is equal to the square root of the difference between the square of the diagonal
from which the height is dropped and the square of the length of the segment between the point from which the
diagonal is drawn and the point of intersection of the height and the base (5)
Problem
The height of a parallelogram is drawn from the vertex of an obtuse angle and is equal to 5 cm. The height bisects the side
of the parallelogram. The acute angle is 30 degrees. Find the diagonal of the parallelogram drawn from the vertex of the
obtuse angle and the angles that it forms with the sides of the parallelogram.
Solution
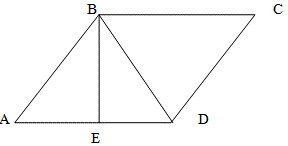
Since, by the condition of the problem, AE=ED, then the triangles ABE and DBE are equal to each other
(by the first sign of equality of triangles: two sides and the angle between them are equal, AE=ED and BE is
a common side, and BE forms an angle of 90 degrees with AD). Thus, the angle ADB is equal to 30 degrees.
Accordingly, the angle DBC is also equal to 30 degrees as an internal cross lying on parallel lines BC and AD.
From the right triangle ABE, we determine that the angle ABE is 180°−90°−30°=60°
Whence (from the equality of triangles ABE and DBE) the angle EBD is also 60 degrees. Thus, the diagonal forms
with the second base the angle ABD=60°+60°=120°.
BDC=ABD=120° as the internal diagonal.
Find the length of the diagonal.
BE / BD = cos ∠EBD
BE / BD = cos 60
Substitute the value of the cosine of 60 degrees and we get:
BE/BD = 1/2
By the condition of the problem, BE=5BE = 5 cm, from which
5/BD = 1/2
BD = 10
Answer: The length of the diagonal of the parallelogram is 10 cm, and the angles that the diagonal forms with
the bases are 30 and 120 degrees.
Parallelogram |
Описание курса
| Trapeze (Trapezoid)
|

