Volume of a Prism

A prism is a polyhedron whose bases are equal polygons and whose lateral faces are parallelograms.
The volume of a prism can be found using a simple formula:

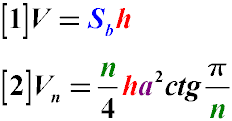
where:

• V is the volume of the prism,
• Sb is the area of the base of the prism,
• h is the height of the prism (the distance between the bases).

Universal Formula for Finding the Volume of Any Prism (1)

To find the volume of a prism, you must first calculate the area of its base. After calculating the area of the base,
it is multiplied by the height of the prism to obtain the volume. This formula is applicable to any prism, regardless of the shape of its base.

Volume of a Prism with a Regular Polygon Base (2)

For a prism with a regular polygon as its base, the volume can be calculated using a more specific formula. If the base is a regular polygon
with nn sides, each of length aa, the area of the base can be found using the formula for the area of a regular polygon.

where (see above):

• n is the number of sides of the regular polygon,
• a is the length of each side.