Список предметов
The cosine theorem and its proof
39 / 79

Formulation and Proof of the Law of Cosines

The Law of Cosines states that the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides minus
twice the product of those sides and the cosine of the angle between them.

The Law of Cosines is a generalization of the Pythagorean theorem for any triangle.

Formulation of the Law of Cosines

For a plane triangle with sides a, b, c and an angle α opposite side aa, the following relationship holds:

Теорема косинусов утверждает, что квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторонна косинус угла между ними.

Изображение для пояснения сути теоремы косинусов - квадрат стороны произвольного треугольника равен сумме квадратов двух других сторон минус удвоенное их произведение на косинус угла между ними

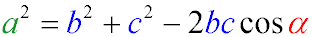
a2=b2+c2−2bc⋅cos⁡(α)

Useful Formulas of the Law of Cosines

Полезные формулы теоремы косинусов - сама теорема, нахождение косинуса угла по трем сторонам и нахождение самого угла по трем сторонам треугольника
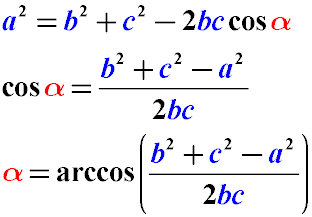
  1. Finding the side of a triangle:
    2. a2=b2+c2−2bc⋅cos⁡(α)
  2. Finding the cosine of an angle given three sides:
    3. cos⁡(α) = b2+c2−a2 / 2bc
  3. Finding the angle given three sides of a triangle:
α = arccos⁡( b2+ c2−a2 / 2bc)

Using the Law of Cosines, one can find not only the side of a triangle given two sides and the angle between them, but also, knowing the lengths of all sides
of the triangle, determine the cosines of all angles and calculate the magnitude of any angle of the triangle. Calculating any angle of a triangle based on its sides
is a consequence of transforming the formula of the Law of Cosines.

Proof of the Law of Cosines

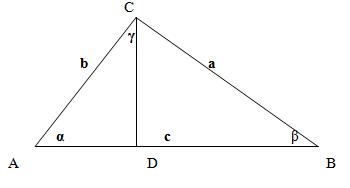
Consider an arbitrary triangle ABC. Suppose we know the length of side AC (denoted as b), the length of side AB (denoted as c), and the angle between these sides,
 denoted as α. We need to find the length of side BC (denoted as a).

To prove the Law of Cosines, we will perform additional constructions. From vertex C, drop a perpendicular CD to side AB.

Теорема Косинусов

  1. Find the length of side AB. As seen from the diagram, as a result of the additional construction, we can say that:
    2. AB = AD+BD
  2. Find the length of segment AD. Given that triangle ADC is a right triangle, we know the length of its hypotenuse (b) and the angle (α).
    The length of side AD can be found using the properties of trigonometric functions in a right triangle:
    3. AD / AC = cos⁡(α)

    Hence,

    AD = AC⋅cos⁡(α)
    AD = b⋅cos⁡(α)
  3. Find the length of segment BDBD as the difference between ABAB and ADAD:
    4. BD = AB − AD
    BD = c − b⋅cos⁡(α)
  4. Apply the Pythagorean theorem to the right triangles ADC and BDC:
    For triangle BDC:
    5. CD2 + BD2 = BC2

    For triangle ADC:

    CD2 + AD2 = AC2
  5. Note that both triangles share the common side CD. Determine its length for each triangle and equate the expressions:
    6. CD2 = BC2  - BD2
    CD2 = AC2 -  AD2
  6. Since the left sides of the equations (the square of side CD) are equal, equate the right sides:
    7. BC2  - BD2 =  AC2 -  AD2
  7. From the previous calculations, we know:
    8. AD = b cos  α
    BD = c − b cos α
    AC = b 

    Let the length of side BC be a:

    BC=a
  8. Substitute the values into the equation:
    9. a2  - (  c − b cos α  )2  =  b2 -  ( b cos α  )2
  9. Expand and simplify:
a2  = (  c − b cos α  )2  +  b2 -  ( b cos α  )2
a2  =   b2 + c 2  - 2c b cos α +  ( b cos α  )2   -  ( b cos α  )2
a2  =   b2 + c 2  - 2bc cos α

Thus, the Law of Cosines is proven.

The case where one of the angles at the base is obtuse (and the height falls on the extension of the base) is entirely analogous to the one considered.

0  


 Cosine | Описание курса | The Law of Cosines. Example of a Problem Solution