The law of cosines is formulated as follows: the square of any side of a triangle is equal to the sum of the squares of the other two sides, minus twice
the product of these sides and the cosine of the angle between them.

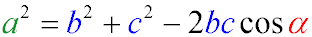
Problem

One side of the triangle is 8 centimeters longer than the other, and the angle between them is 120 degrees. Find the perimeter of the triangle if the length
of the third side is 28 cm.

Solution.

Let's designate one side of the triangle as x, then the value of the other is x+8 cm.

Based on the cosine theorem, we get:

28² = x² + (x+8)²-2x(x+8)cos120^o
784 = x² + x² +16x + 64 - 2x(x+8)(-0,5)
784 = 2x²+16x + 64 + x(x+8)
720 = 3x² + 16x + 8x
3x² + 24x +720 = 0
D=9216
x₁=((-24)+96)/6=12 (the second root is a negative number and has no meaning in the context of solving the problem)

Thus, the perimeter of the triangle P=12+(12+8)+28 = 60 см.

Answer: 60 см

Problem

In triangle ABC, side AC is equal to 7√3 cm, side BC is equal to 1 cm. Angle C is equal to 150 degrees. Find the length of side AB.

Solution.

Let's apply the cosine law and the corresponding formula (see above)
AB²  = (7√3)² + 1²  - 2 (7√3) cos 150º

We will find the value of the cosine of 150 degrees using the table of values ​​of trigonometric functions.
AB² = 147 + 1 - 14√3 (-√3/2) 
AB² = 148 + 21 = 169
AB = 13

Answer: 13 cm