Hypotenuse of a Right Triangle

The hypotenuse is the side of a right triangle opposite the right angle. It is the longest side of the triangle.

Properties of the Hypotenuse

1. Longest Side: The hypotenuse is the longest side of a right triangle.
2. Circumscribed Circle: If a circle is circumscribed around a right triangle, then the hypotenuse is the diameter of such a circle, and its center
   bisects the hypotenuse.

Formulas for Finding the Length of the Hypotenuse

In the figure, the hypotenuse of a right triangle is marked in red.

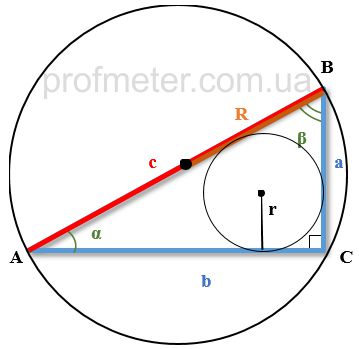
Notation:

• c - hypotenuse of a right triangle
• a, b - legs of a right triangle
• α,β - acute angles
• R - radius of the circumscribed circle
• r - radius of the inscribed circle

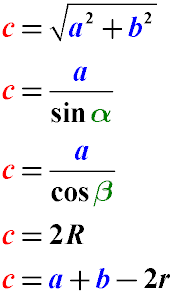
Formulas for finding the length of the hypotenuse through the legs, leg and angle, radius of the inscribed and circumscribed circle:

1. Pythagorean Theorem: The length of the hypotenuse of a right triangle is equal to the square root of the sum of the squares of the legs
2. Through the Leg and the Opposite Angle: The length of the hypotenuse is equal to the length of the leg divided by the sine of the angle
   opposite to it
3. Through the Leg and the Adjacent Angle: The length of the hypotenuse is equal to the length of the leg divided by the cosine of the angle
   adjacent to it
4. By the Radius of the Circumscribed Circle: The length of the hypotenuse is equal to twice the radius of the circle circumscribed around
   a right triangle
5. By the Radius of the Inscribed Circle: The length of the hypotenuse of a right triangle is equal to the sum of the legs of this triangle minus
   twice the radius of the inscribed circle

Additional Information

• Relationship with the Circumscribed Circle: The hypotenuse being the diameter of the circumscribed circle means that the right angle of
  the triangle subtends a semicircle. This property is useful in various geometric proofs and constructions.
• Applications: The hypotenuse is a fundamental concept in trigonometry and geometry, used in calculating distances, angles, and in various
  real-world applications such as construction, navigation, and physics.