Quadrilateral side length properties

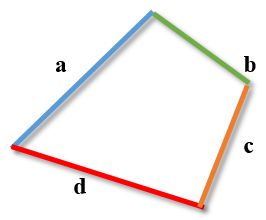
The modulus of the difference of any two sides of a quadrilateral does not exceed the sum of its other two sides.

|a -b| ≤ c + d
|a -c| ≤ b + d
|a -d| ≤ b + c
|b -c| ≤ a + d
|b -d| ≤ a + b
|c -d| ≤ a + b

In any quadrilateral, the sum of the lengths of its three sides is not less than the length of the fourth side.

a ≤ b + c + d
b ≤ a + c + d
c ≤ a + b + d
d ≤ a + b + c

Important. When solving problems within the school curriculum, you can use strict inequality (<). 
Equality is achieved only if the quadrilateral is "degenerate", that is, its three points lie on the same straight line. 
That is, this situation does not fall under the classical definition of a quadrilateral.

Problem on the Possibility of the Existence of a Quadrilateral with Given Sides

Problem 1

Does a quadrilateral exist if the lengths of the sides are 1 cm, 3 cm, 5 cm, and 9 cm?

Solution:

In order for a quadrilateral to exist, the length of any one of its sides must be less than the sum of the lengths of the other three sides.
Otherwise, it will be impossible to close the perimeter.

To check, we take the largest of the sides (9 cm). Then the sum of the remaining sides will be:

This means that the length of the largest side (9 cm) is equal to the sum of the other three sides. In this case, it is impossible to form a closed
quadrilateral because the sides would lie on a straight line.

Conclusion: Such a quadrilateral cannot exist.

Answer: No, it does not exist.

Problem 2

Does a quadrilateral exist if the lengths of the sides are 5 cm, 17 cm, 3 cm, and 7 cm?

Solution:

For a quadrilateral to exist, the length of any one of its sides must be less than the sum of the lengths of the other three sides.
Otherwise, it will be impossible to close the perimeter.

To check, we take the largest of the sides (17 cm). Then the sum of the remaining sides will be:

This means that the length of the largest side (17 cm) is greater than the sum of the other three sides.
In this case, it is impossible to form a closed quadrilateral because the largest side would be too long to connect with the other sides.

Conclusion: Such a quadrilateral cannot exist.

Answer: No, it does not exist.