Definition of a Chord

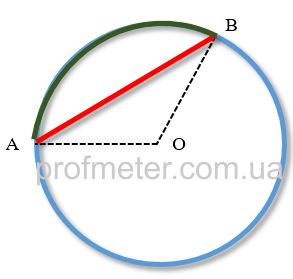
A chord is a segment that connects two points on a given curve. A chord can be part of various geometric shapes, such as an arc, a circle, an ellipse, etc.
In the figure, the chord is indicated as a red segment AB. Both of its ends are on the circle.

The part of the curve enclosed between two points of the chord is called an arc. In the figure, the arc of the chord AB is indicated in green.

A segment is a flat figure enclosed between an arc and its chord. The segment in the figure is bounded by the red segment AB on one side and
the green arc on the other side.

The chord passing through the center of the circle is called the diameter of the circle. The diameter of a circle is the longest chord of the circle.

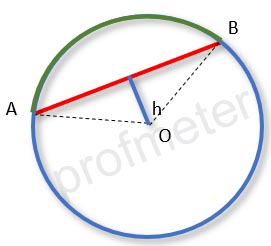
Properties of a Chord of a Circle

1. If the distances from the center of the circle to the chords (h) are equal, then these chords are equal.
   The converse is also true: if the chords are equal, then the distances from the center of the circle to these chords (h) are equal.
2. If the chord is longer, then the distance from the center of the circle to this chord (h) is shorter.
   Conversely, if the chord is shorter, then the distance from the center of the circle to this chord (h) is longer.
3. The largest possible chord is the diameter.
4. The median perpendicular to the chord passes through the center of the circle.
5. If the diameter bisects a chord that is not a diameter, then this diameter is perpendicular to this chord.
   Conversely, if the diameter is perpendicular to a chord, then this diameter bisects this chord.
6. If the diameter bisects a chord that is not a diameter, then this diameter bisects the arcs that are subtended by this chord.
   Conversely, if the diameter bisects an arc, then this diameter bisects the chord that subtends this arc.
7. If the radius bisects a chord that is not a diameter, then this radius is perpendicular to this chord.
   Conversely, if a radius is perpendicular to a chord, then this radius bisects this chord.
8. If a radius bisects a chord that is not a diameter, then this radius bisects the arc subtended by this chord.
   Conversely, if a radius bisects an arc, then this radius bisects the chord that subtends this arc.
9. If a radius is perpendicular to a chord, then this radius bisects the arc subtended by this chord.
   Conversely, if a radius bisects an arc, then this radius is perpendicular to the chord that subtends this arc.

Properties of Chord and Inscribed Angle

In figure [1], the inscribed angle is denoted as ∠ACB, and the chord of the circle is AB.

1. If the inscribed angles are subtended by the same chord and the vertices of these angles lie on the same side of this chord,
   then these angles are equal.
2. If a pair of inscribed angles are subtended by the same chord and the vertices of these angles lie on different sides of this chord,
   then the sum of these angles is 180°.
3. If the inscribed and central angles are subtended by the same chord and the vertices of these angles lie on the same side of this chord,
   then the inscribed angle is equal to half the central angle.
4. If the inscribed angle is subtended by the diameter, then this angle is a right angle.

Properties of Chord and Central Angle

In figure [2], the central angle is denoted as ∠AOB, and the chord as AB.

1. If chords subtend equal central angles, then these chords are equal.
2. If the chords are equal, then these chords subtend equal central angles.
3. A larger chord subtends a larger central angle, and a smaller chord subtends a smaller central angle.
4. A larger central angle is subtended by a larger chord, and a smaller central angle is subtended by a smaller chord.

Formulas for Finding Chords

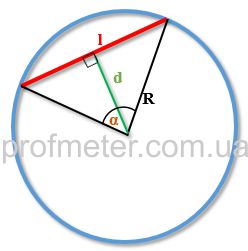
Symbols of chord, perpendicular, central angle, and circle radius for use in formulas:

• l is the length of the chord
• α is the value of the central angle
• R is the radius of the circle
• d is the length of the perpendicular drawn from the center of the circle to the chord

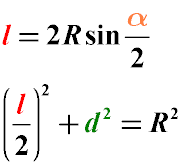
1. The length of the chord of a circle (l) is equal to twice the radius of the given circle (R) multiplied by the sine of half the central angle:
2. The sum of the square of half the length of a chord and the square of the perpendicular drawn to that chord is equal to the square
   of the radius of the circle. This formula follows from the Pythagorean theorem

Problem Solving

Task

Chords AB and CD intersect at point S, where AS:SB=2:3, DS = 12 cm, SC = 5 cm.
Find AB.

Solution

1. Understand the given information:
   • AS: SB = 2: 3
   • DS = 12 cm
   • SC = 5 cm
2. Use the given ratio to express AS and SB: Let AS = 2x and SB = 3x.
3. Find the total length of ABAB:

• Apply the intersecting chords theorem:
  The intersecting chords theorem states that the product of the segments of one chord is equal to the product of the segments of the other chord.
  Therefore:

• Substitute the known values:

• Solve for x:

• Find the length of AB:

Answer

The length of AB is 5√10 cm.

Task

A circle is divided into parts that are related as 3.5: 5.5: 3, and the points of division are connected to each other.
Determine the size of the angles of the formed triangle.

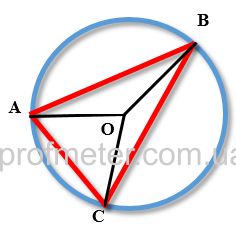
Solution

1. Understand the given ratios: The circle is divided into three parts with the ratios 3.5: 5.5: 3.
   These ratios represent the angles at the center of the circle formed by the segments connecting the points of division.

2. Calculate the angles at the center: The total angle around a point (center of the circle) is 360 degrees.
   We need to find the angles corresponding to the given ratios.
   The sum of the ratios is:

The angles at the center are proportional to these ratios: