Isosceles Triangle

Definition

An isosceles triangle is a triangle in which the lengths of two of its sides are equal to each other.

Note: From the definition of an isosceles triangle, it follows that a right triangle can also be isosceles if its two legs are equal. However, it must be
remembered that the converse statement is false; not all isosceles triangles are right triangles.

Properties of an Isosceles Triangle

The properties given below are used in solving problems. Since they are widely known, it is assumed that they do not require explanation. Therefore,
references to them are absent in the texts of the problems.

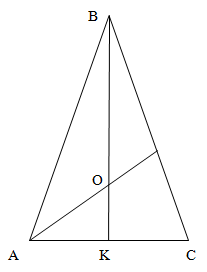
1. The angles opposite the equal sides of an isosceles triangle are equal to each other.
2. The bisectors, medians, and altitudes drawn from the angles opposite the equal sides of the triangle are equal to each other.
3. The bisector, median, and altitude drawn to the base coincide with each other.
4. The centers of the inscribed and circumscribed circles lie on the altitude, bisector, and median (they coincide) drawn to the base.
5. The angles opposite the equal sides of an isosceles triangle are always acute.

Formulas for Finding the Sides of an Isosceles Triangle

The sides of a triangle can be calculated using formulas that express their length in terms of other sides and angles, the magnitude
of which is known.

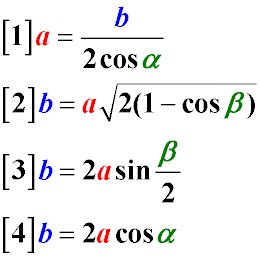
1. The lateral side of an isosceles triangle is equal to the fraction of the base divided by the double cosine of the angle at the base [1]. 
   This identity can be obtained by simple transformations from the cosine theorem.
2. The base of an isosceles triangle is equal to the product of the side by the square root of the doubled difference of unity and the
   cosine of the angle at the vertex [2]
3. The base of an isosceles triangle is equal to the doubled product of the side by the sine of half the angle at the vertex [3]
4. The base of an isosceles triangle is equal to the doubled product of the side by the cosine of the angle at its base [4]

Radius of the Inscribed Circle in an Isosceles Triangle

Formulas for finding the radius of the inscribed circle for an isosceles triangle through angles, sides, and height:

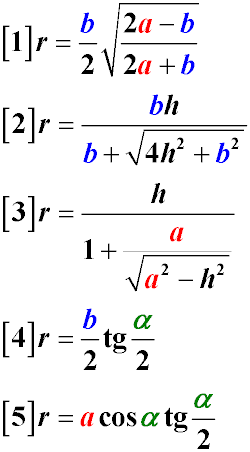
1. The radius of the inscribed circle for an isosceles triangle can be found based on the values ​​of the base and each side. (Formula 1)
2. The radius of the inscribed circle for an isosceles triangle can be determined based on the values ​​of the base and the height drawn
   to the base (Formula 2)
3. The radius of the inscribed circle in a triangle can also be calculated using the length of a side and the height drawn to the base
   of the triangle (Formula 3)
4. Knowing the size of the angle between the sides and the length of the base also allows you to determine the radius of the inscribed
   circle (Formula 4)
5. A similar formula (5) allows you to determine the radius of the inscribed circle using the sides and the angle between them

Signs of an Isosceles Triangle

A triangle that has the following signs is isosceles:

1. Two angles of a triangle are equal to each other.
2. The height coincides with the median.
3. The height coincides with the bisector.
4. The bisector coincides with the median.
5. Two heights are equal to each other.
6. Two medians are equal to each other.
7. Two bisectors are equal to each other.

Area of an Isosceles Triangle

The area of an isosceles triangle can be found using the following formulas:

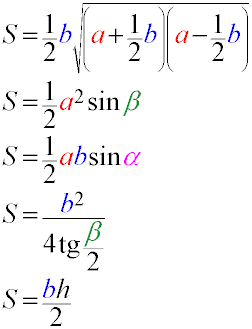
• Using the base and height
• Using the sides and the angle between them
• Using the base and the angles at the base

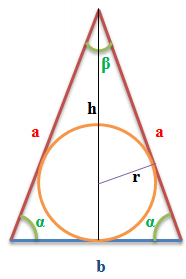
Where:

• a is the length of one of the two equal sides of the triangle.
• b is the length of the base.
• α (alpha) is the size of one of the two equal angles at the base.
• β (beta)  is the size of the angle between the equal sides of the triangle and opposite the base.