Task:

In triangle ABC, medians CD and BE intersect at point K.
Find the area of quadrilateral ADKE if BC = 20 cm, AC = 12 cm, and angle ACB is 135 degrees.

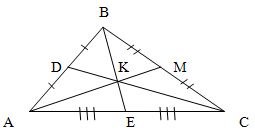
Solution:

1. Properties of Medians:
   • The medians of a triangle intersect at a point called the centroid, which divides each median into two parts in a 2:1 ratio from the vertex.
   • The triangle is divided by the three medians into six equal-area triangles.

2. Area of the Triangle:

   • The area of the triangle can be found using the formula S=1/2 ab sin⁡ γ, where a and b are the sides of the triangle, and γ is the included angle.
   • Given BC = 20 cm, AC = 12 cm, and ∠ACB=135°:

• The value of sine 135 degrees: sin⁡135° = √2/2

1. Area of Quadrilateral ADKE:
   • The quadrilateral ADKE is formed by two of the six equal-area triangles.
   • Therefore, its area is 1/3 of the total area of the triangle:

Answer: The area of quadrilateral ADKE is 20√2 cm².