|
|
A regular pyramid is a special case of a pyramid.
Right (regular) pyramid. Definition
Definition 1. A pyramid is called regular if its base is a regular polygon, and the top of such a pyramid is projected into the center of its base.
Definition 2. A pyramid is called regular if its base is a regular polygon, and the height passes through the center of the base.
Definition 3. A regular pyramid is a right pyramid whose base is a regular polygon.
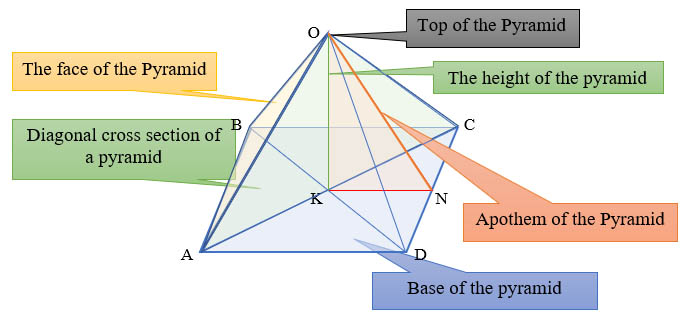
Elements of a regular pyramid
- The height of a side face drawn from its vertex is called apothem. In the figure it is designated as segment ON
- The point connecting the side edges and not lying in the plane of the base is called the top of the pyramid (O)
- Triangles that have a common side with the base and one of the vertices coinciding with the vertex are called side faces (AOD, DOC, COB, AOB)
- The segment of the perpendicular drawn through the top of the pyramid to the plane of its base is called the height of the pyramid (OK)
- The diagonal section of a pyramid is the section passing through the apex and base diagonal (AOC, BOD)
- A polygon that does not belong to the top of the pyramid is called the base of the pyramid (ABCD)
If the base of a regular pyramid is a triangle, quadrilateral, etc. then it is called regular triangular, quadrangular, etc.
A triangular pyramid is a tetrahedron.
Properties of a regular pyramid
To solve problems, it is necessary to know the properties of individual elements, which are usually omitted in the condition, since it is believed that the student should know this from the very beginning.
- side ribs are equal to each other
- apothems are equal
- the side faces are equal to each other (at the same time, their areas, sides and bases are equal, respectively), that is, they are equal triangles
- all side faces are congruent isosceles triangles
- in any regular pyramid, you can both inscribe and describe a sphere around it
- if the centers of the inscribed and circumscribed spheres coincide, then the sum of the plane angles at the top of the pyramid is equal to π, and each of them, respectively, is π/n, where n is the number of sides of the base polygon
- the area of the lateral surface of a regular pyramid is equal to half the product of the perimeter of the base and the apothem
- a circle can be circumscribed near the base of a regular pyramid (see also the radius of the circumscribed circle of a triangle)
- all side faces form equal angles with the base plane of a regular pyramid
- all heights of the side faces are equal to each other
Instructions for solving problems. The properties listed above should help in a practical solution.
If you need to find the angles of inclination of the faces, their surface, etc., then the general technique is to split
the entire three-dimensional figure into separate flat figures and use their properties
to find individual elements of the pyramid, since many elements are common to several figures.
It is necessary to break the entire three-dimensional figure into separate elements - triangles, squares, segments. Further, to apply knowledge from the planimetry course to individual elements, which greatly simplifies finding the answer.
Formulas for a regular pyramid
Formulas for finding volume and lateral surface area:
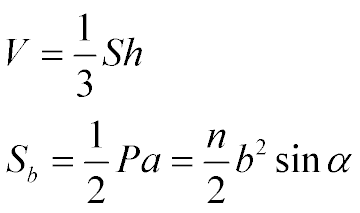
Designations:
V - volume of the pyramid
S - base area
h - the height of the pyramid
Sb - side surface area
a - apothem (not to be confused with α)
P - base perimeter
n - number of base sides
b - side rib length
α - flat angle at the top of the pyramid
This formula for finding volume can only be used for a regular pyramid:
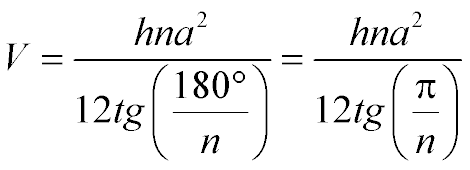 , где , где
V - volume of a regular pyramid
h - the height of the regular pyramid
n is the number of sides of the regular polygon that is the base for the regular pyramid
a - side length of a regular polygon
Regular truncated pyramid
If we draw a section parallel to the base of the pyramid, then the body enclosed between these planes and the side surface is called a truncated pyramid.
This section for a truncated pyramid is one of its bases.
The height of the side face (which is an isosceles trapezoid) is called the apothem of a regular truncated pyramid.
A truncated pyramid is called correct if the pyramid from which it was obtained is correct.
The distance between the bases of a truncated pyramid is called the height of the truncated pyramid
All faces of a regular truncated pyramid are isosceles (isosceles) trapezoids
Pyramid. Problem solving |
Описание курса
| Regular pyramid with a quadrilateral base
|

