Sine, cosine and tangent of angle 15 degrees

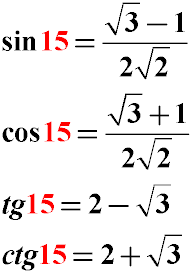
How to find the values of trigonometric functions for an angle of 15 degrees

Find the values of the sine, cosine and tangent for an angle of 15 degrees in an analytical way.
At first glance, finding the values of the sine, cosine and tangent for an angle of 15 degrees is a difficult task. However, this is not quite true.
The formulas for transforming the double angle of trigonometric functions will come to our aid.

The fact is that we can imagine an angle of 30 degrees, like a double angle of 15 degrees ( 2 * 15 ).

Then, starting from the identity:
cos 2α = 1 - 2sin²α

We take a double angle as 2 * 15 degrees, then
cos 30 = 1 - 2sin²15
sin²15 = ( 1 - cos 30 ) / 2

The cosine value for a 30 degree angle is easy to calculate. It is equal to √3/2
sin²15 = ( 1 - √3/2 ) / 2
sin 15 = √ (( 1 - √3/2 ) / 2 )
The upper part of the fraction under the root will be reduced to the common denominator (2)
sin 15 = √ ((  (2 - √3) /2 ) / 2 ) = √(  (2 - √3) / 4 )
now we have one fraction under the root sign. We multiply the numerator and denominator by two
sin 15 = √(  (2 - √3) / 4 ) = √( (4 - 2√3) / 8 )
the most interesting moment, we can imagine 4 - 2√3 as (√3-1)²
then
sin 15 = √( (√3-1)² / 8 ) = (√3-1)/ √8 = (√3-1)/ (2√2)

by simple algebraic transformations we obtain:

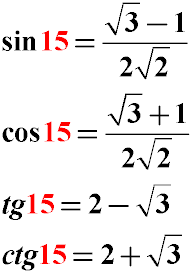
As can be seen from the example, the values of the trigonometric functions of the sine, cosine and tangent angles of 15 degrees can be obtained by simple trigonometric transformations using trigonometric identities of the transformations of double angles and halves of given angles.

See also the full table of values of trigonometric functions (table of sines, cosines and tangents).

Below are also the values of trigonometric functions for an angle of 15 degrees in the form of a decimal fraction with four decimal places.

π/12	sine of 15  sin 15	cosine of 15 cos 15	tangent of 15 tg 15	cotangent of 15 ctg 15
Value	0.2588190451	0.96592582628	0.26794919243	3.73205080757