Properties of the Median of a Right Triangle

Definition of the Median

The median of a triangle is a segment connecting one of the vertices of the triangle with the midpoint of the side opposite to it.
The median is also called the line containing this segment. The medians of a triangle intersect at one point and are divided by
this point into two parts in a ratio of 2:1, counting from the vertex of the angle. The point of their intersection is called the
center of gravity of the triangle (relatively rarely in problems, the term "centroid" is used to denote this point).

Key Properties of the Median

• The median divides the triangle into two equal triangles.

• A triangle is divided by three medians into six equal triangles.

• The larger side of the triangle corresponds to the smaller median.

Formulas of the Properties of the Median in a Right Triangle

The geometry problems proposed for solution mainly use the following properties of the median of a right triangle:

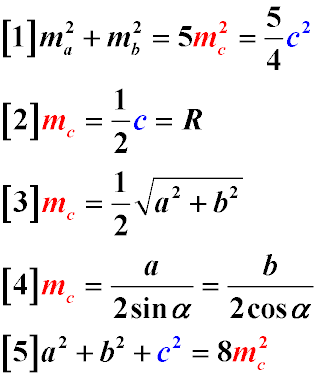
1. The sum of the squares of the medians dropped onto the legs of a right triangle is equal to five squares of the median
   dropped onto the hypotenuse (1)

2. The median dropped onto the hypotenuse of a right triangle is equal to half the hypotenuse (2)

3. The median dropped onto the hypotenuse of a right triangle is equal to the radius of the circle circumscribed around
   the right triangle (2)

4. The median dropped onto the hypotenuse is equal to half the square root of the sum of the squares of the legs (3)

5. The median dropped onto the hypotenuse is equal to the quotient of dividing the length of the leg by two sines of the
   opposite leg of the acute angle (4)

6. The median dropped onto the hypotenuse is equal to the fraction of dividing the length of the leg by two cosines of
   the adjacent leg of the acute angle (4)

7. The sum of the squares of the sides of a right triangle is equal to eight squares of the median dropped onto its
   hypotenuse (5)

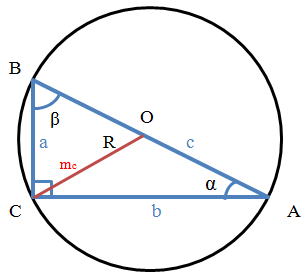
Notation in the Formulas

• a, b: Legs of a right triangle.

• c: Hypotenuse of a right triangle.

• If we denote the triangle as ABC, then:

  • BC = a

  • AC = b

  • AB = c

  • (i.e., sides a, b, c are opposite to the corresponding angles)

• m_a: Median drawn to leg a.

• m_b: Median drawn to leg b.

• m_c: Median of a right triangle drawn to hypotenuse c.

• α (alpha): Angle CAB opposite to side a.

Problem about the median in a right triangle

a and b, and the hypotenuse as c. The medians drawn to the legs are given as 3 cm and 4 cm, respectively.

We know the following properties of the medians in a right triangle:

1. The sum of the squares of the medians drawn to the legs is equal to five times the square of the median drawn to
   the hypotenuse:

2. The median drawn to the hypotenuse is equal to half the hypotenuse:

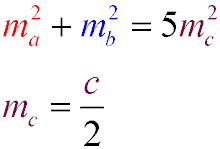
Given:

Using the first property:

Using the second property:

Therefore, the hypotenuse of the triangle is 2√5≈4.472

Answer: The hypotenuse of the triangle is 2√5 cm.