|
|
Parallelogram: Definition, Properties, and Calculations
A parallelogram is a quadrilateral whose opposite sides are parallel in pairs, meaning they lie on parallel lines.
Special Cases of Parallelograms
Special cases of parallelograms include:
-
Rectangle: A parallelogram with four right angles.
-
Square: A parallelogram with four right angles and all sides equal.
-
Rhombus: A parallelogram with all sides equal.
What Does a Parallelogram Look Like?
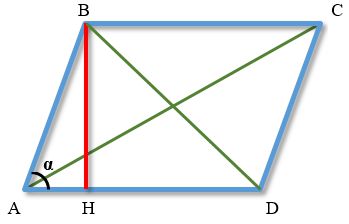
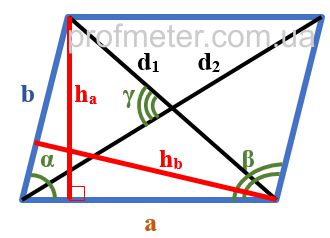
A parallelogram with a height drawn to one of the bases and diagonals.
In the figure above, the parallelogram is marked with blue lines.
Elements of a Parallelogram
-
ABCD: A parallelogram whose opposite sides are parallel in pairs (AB is parallel to CD, and BC is parallel to AD).
-
BH: The height of the parallelogram dropped from point B to the base AD (marked in red in the figure).
-
AC and BD: The diagonals of the parallelogram.
Properties of a Parallelogram
-
Opposite sides of a parallelogram are equal.
-
Opposite angles of a parallelogram are equal.
-
The diagonals of a parallelogram intersect and are bisected by the point of intersection. The point of intersection
of the diagonals is called the center of symmetry of the parallelogram.
-
The diagonal divides the parallelogram into two equal triangles.
-
The sum of the angles adjacent to one side is 180°.
-
The sum of all angles is 360°.
-
The midlines of a parallelogram intersect at the point of intersection of its diagonals and are divided in half by this point.
-
The sum of the squares of the diagonals of a parallelogram is equal to twice the sum of the squares of its sides.
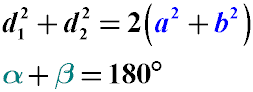
Parallelogram Characteristics
A quadrilateral ABCD is a parallelogram if one of the following conditions is met:
- Opposite sides are pairwise equal.
-
Opposite sides are pairwise parallel and equal.
-
Opposite angles are pairwise equal.
-
Diagonals are bisected at their intersection point.
-
The sum of adjacent angles is 180 degrees.
-
Two sides are equal and parallel.
How to Find the Area of a Parallelogram
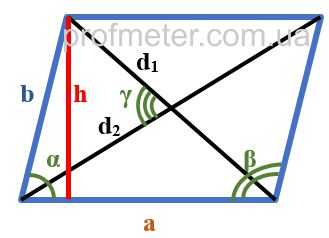
The formulas for finding the area of a parallelogram are given below:
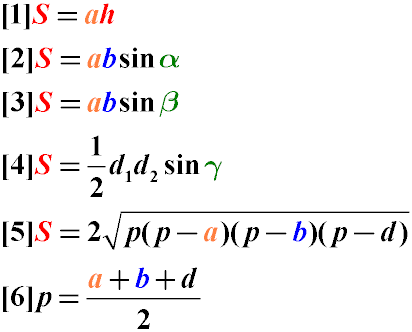
-
The area of a parallelogram is equal to the product of the length of one of its sides by the height dropped to this side (1).
-
The area of a parallelogram is equal to the product of its two adjacent sides by the sine of the angle between them (2,3).
-
The area of a parallelogram is equal to half the product of its diagonals by the sine of the angle between them (4).
-
The area of a parallelogram can also be found using Heron's formula, considering one of the diagonals as a triangle
and calculating the doubled area of this triangle (5).
How to Find the Sides of a Parallelogram
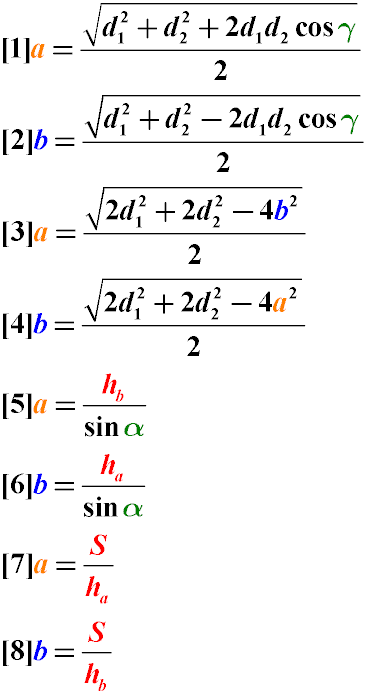
The sides of a parallelogram can be found through:
-
The sizes of the diagonals and the angle between them (1,2).
-
The lengths of the diagonals and one of the sides (3,4).
-
The height dropped onto the side and the angle between the sides (5,6).
-
The area and height dropped onto a given side (7,8).
How to Find the Diagonals of a Parallelogram

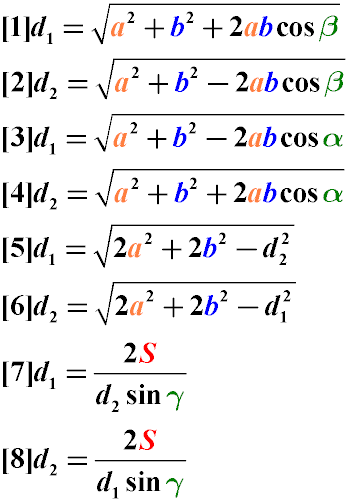
The diagonal of a parallelogram can be found through:
-
The lengths of its sides and the cosine of the angle between them (1,2,3,4).
-
The lengths of the sides and the size of the second diagonal (5,6).
-
The area, the length of the second diagonal, and the angle between them (7,8).
How to Find the Perimeter of a Parallelogram

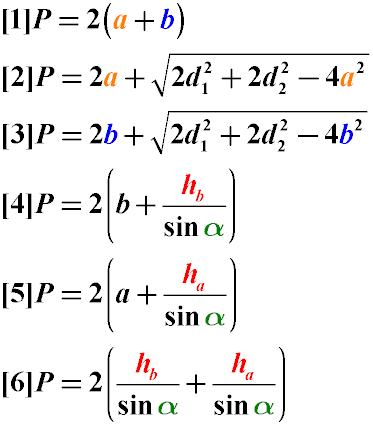
The perimeter of a parallelogram can be found:
-
By its sides (1).
-
By one of the sides and the length of two diagonals (2,3).
-
By the side, height, and angle between the sides (4,5,6).
Existence of a quadrilateral with given sides |
Описание курса
| Height of parallelogram
|

