Problem. The axial section of the cylinder is a square whose diagonal is 4 cm. Find the volume of the cylinder

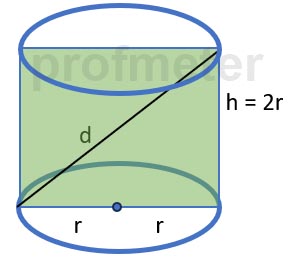
To solve this problem, let's break it down step by step:

1. Find the side length of the square cross-section:
   • The diagonal of the square is given as 4 cm.
   • For a square, the relationship between the side length a and the diagonal d is given by the formula:


• Solving for a:
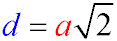
a = d / √2= 4 / √2 = 2√2 cm


2. Determine the radius of the cylinder:

   • The side length of the square is equal to the diameter of the cylinder's base.
   • Therefore, the radius rr of the cylinder is:
r = a / 2 = 2√2 / 2 = √2 cm


3. Find the height of the cylinder:

   • The height hh of the cylinder is equal to the side length of the square cross-section:
h = 2√2 cm


4. Calculate the volume of the cylinder:

   • The volume V of a cylinder is given by the formula:



• Substituting the values:

So, the volume of the cylinder is 4√2π cm³

Problem

Find the total surface area of a cylinder if the diagonal of its axial section, which is 8 cm, forms an angle of 30 degrees
with the generator of the cylinder.

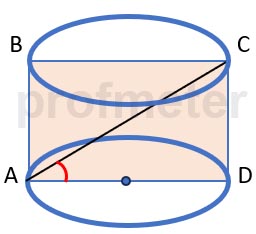
Solution

The cylinder has an axial section in the form of a parallelogram with the given diagonal angle.

Since AC = 8 cm and the angle ACD = 30°, then:

Explanation: Triangle ACD is a right triangle. Therefore, CD/AC=cos⁡(∠ACD) by the property of trigonometric functions in a right triangle.
The value of cos⁡(30°) can be found from the table of trigonometric function values.

Similarly,

From this, the radius of the base of the cylinder is:

The area of the base of the cylinder is:

The lateral surface area of the cylinder is the area of its development - the product of the circumference of the base and the height of the cylinder.
That is:

The total surface area of the cylinder is:

Answer: 4π+16π√3