|
|
Task 1. Find the volume of the pyramid
The diagonal of the base of a regular quadrilateral pyramid is 4 cm, and the lateral face forms an angle of 60 degrees with the base.
Find the volume of the pyramid.
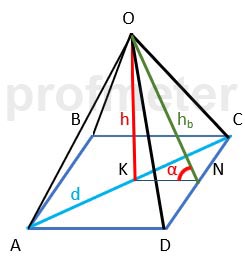
Let's solve the problem step by step:
-
Find the side of the base of the pyramid:
- The base of a regular quadrilateral pyramid is a square.
-
The diagonal of the square d is related to the side aa by the formula: d=a√2
-
The diagonal d = 4 cm, therefore:
4 = a√2 ⟹ a = 4 / √2 =2√2 cm
- Find the height of the lateral face of the pyramid:
- The height of the lateral face hb forms an angle of 60 degrees with the base.
-
The height of the lateral face hb is the hypotenuse of a right triangle, where one of the legs is equal to half the side of the base a/2,
-
and the other leg is the height of the pyramid h.
-
We use the trigonometric cosine function:
cos 60°=( a/2 ) / hb
1/2=2√2/2 / hb
hb= 2√2
- Find the height of the pyramid:
- We use the trigonometric sine function:
sin60°=h / hb
√3/2 = h / 2√2
h = 2√2⋅ √3/2 =√6 cm
- Find the volume of the pyramid:
- The volume of the pyramid V is calculated by the formula:
V=1 / 3 Sbase⋅h
- The area of the base Sbase of a square with side a=2√2:
Sbase=(2√2)2=8 cm2
- Therefore, the volume of the pyramid:
V=1 / 3 ⋅ 8 ⋅ √6 = 8 √6 / 3 cm3
Answer: The volume of the pyramid is 8√6 / 3 cm³.
Problem 2
The side of the base of a regular quadrilateral pyramid is a. The dihedral angles at the base are α.
Find the total surface area of the pyramid.
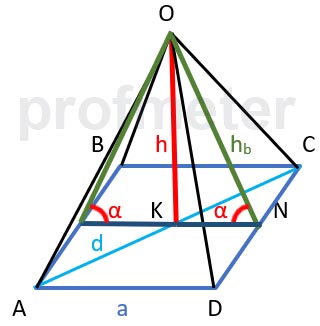
Solution:
To find the total surface area of a regular quadrilateral pyramid, you need to find the area of its base and the area of all lateral faces.
- Area of the base: The base of a regular quadrilateral pyramid is a square with side a. The area of the square is calculated by the formula:
Sbase = a2
- Area of lateral faces: Each lateral face of a regular quadrilateral pyramid is an isosceles triangle. The height of these triangles
is dropped from the vertex of the pyramid to the middle of the side of the base. Let us denote the height of the triangle as hb.
The height hb can be found using the dihedral angle α at the base. The height of the triangle will be:
hb = a / 2⋅cos(α)
The area of one triangle is calculated by the formula:
Striangle = 1/2⋅a⋅hb=1 / 2⋅a⋅( a / 2⋅cos(α) )=a2⋅cos(α) / 4
Since the pyramid has four lateral faces, the total area of the lateral faces will be:
Slateral=4⋅Striangle = 4⋅a2⋅cos(α) / 4= a2⋅cos(α)
- Complete surface area: The total surface area of a pyramid is equal to the sum of the area of the base and the area of the lateral faces:
Stotal=Sbase+Slateral=a2+a2⋅cos(α)=a2(1+cos(α))
Therefore, the total surface area of a regular quadrilateral pyramid is a2(1+cos(α))
Regular pyramid with a quadrilateral base |
Описание курса
| Finding the angles of a regular quadrangular pyramid
|

