Sine, cosine and tangent of angle 120 degrees

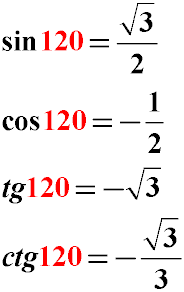
Sine, cosine and tangent of angle 2π / 3 radians

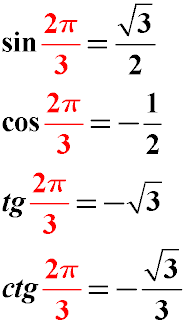
Let us remind ourselves that 2π / 3 in degrees is 120 degrees.  (2 * 180/3 = 120). Thus, to find the value of the trigonometric function for the angle 2π / 3 and for the angle of 120 degrees is the same.

How to find the values of trigonometric functions for an angle of 120 degrees

Find the values of the sine, cosine and tangent for an angle of 120 degrees in an analytical way.
At first glance, finding the values of the sine, cosine and tangent for an angle of 120 degrees is a difficult task. However, this is not quite true.
First of all, we must pay attention that for angles whose values exceed 90 degrees, we have formulas for reducing to an angle less than 90 degrees..

Therefore, to begin with, imagine an angle of 120 degrees as (90 + 30)
Then
sin ( 90 + α ) = cos α
sin 120 = sin( 90 + 30 ) = cos 30

cos ( 90 + α ) = - sin α
cos 120 = cos( 90 + 30 ) = -sin 30

tg ( 90 + α ) = -ctg α
tg 120 = tg( 90 + 30 ) = -ctg 30

Now you can see the values in the sine, cosine and tangent tables 1of 120 degrees, which is converted to trigonometric functions of the sine, cosine and tangent of the angle of 30 degrees.
In the lesson you can see how to calculate the values of trigonometric functions for an angle of 30 degrees.

As a result, we get:

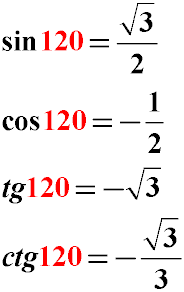
As can be seen from the example, the values of the trigonometric functions of the sine, cosine and tangent angles 120 degrees can be obtained by simple trigonometric transformations using trigonometric identities.

See also the full table of values for trigonometric functions (table of sines, cosines and tangents).

Below are also the values of trigonometric functions for an angle of 120 degrees in the form of a decimal fraction with four decimal places.

2π/3	sine 120  sin 120	cosine 120 cos 120	tangent 120 tg 120	cotangent 120 ctg 120
Value	0,8660	-0,5000	-1,7321	-0,5774