|
|
Diagonals of a trapezoid
Trapezoid Diagonal Properties
- The segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of the bases
- Тthe triangles formed by the bases of the trapezoid and the segments of the diagonals up to the point of their intersection are similar
- Triangles formed by segments of the diagonals of a trapezoid, the sides of which lie on the sides of the trapezoid - equal area (have the same area)
- If we extend the sides of the trapezoid towards the smaller base, then they will intersect at one point with the straight line connecting the midpoints of the bases
- The segment connecting the bases of the trapezoid, and passing through the point of intersection of the diagonals of the trapezoid, is divided by this point in a proportion equal to the ratio of the lengths of the bases of the trapezoid
- A segment parallel to the bases of the trapezoid and drawn through the intersection point of the diagonals is bisected by this point, and its length is equal to 2ab / (a + b), where a and b are the bases of the trapezoid
Properties of a segment connecting the midpoints of the diagonals of a trapezoid
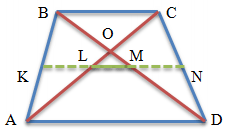
Connect the midpoints of the diagonals of the trapezoid ABCD, as a result of which we will have a segment LM.
The segment connecting the midpoints of the diagonals of the trapezoid lies on the midline of the trapezoid.
This segment is parallel to the bases of the trapezium.
The length of the segment connecting the midpoints of the diagonals of a trapezoid is equal to the half-difference of its bases.
LM = (AD - BC)/2
или
LM = (a-b)/2
Properties of triangles formed by the diagonals of a trapezoid
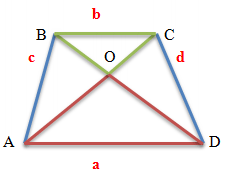
The triangles that are formed by the bases of the trapezoid and the point of intersection of the diagonals of the trapezoid are similar.
Triangles BOC and AOD are similar. Because the angles BOC and AOD are vertical, they are equal.
Angles OCB and OAD are internal crosswise lying at parallel lines AD and BC (the bases of the trapezium are parallel to each other)
and the secant line AC, therefore, they are equal.
Angles OBC and ODA are equal for the same reason (internal cross-lying).
Since all three angles of one triangle are equal to the corresponding angles of another triangle, these triangles are similar.
What follows from this?
To solve problems in geometry, the similarity of triangles is used as follows.
If we know the lengths of the two corresponding elements of similar triangles, then we find the similarity coefficient (we divide one by the other).
From where the lengths of all other elements are related to each other by exactly the same value.
Properties of triangles lying on the lateral side and diagonals of a trapezoid
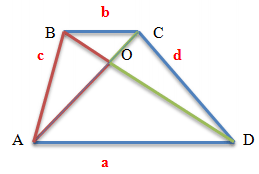
Consider two triangles lying on the sides of the trapezoid AB and CD.
These are triangles AOB and COD. Despite the fact that the dimensions of the individual sides of these triangles can be completely different,
the areas of the triangles formed by the sides and the point of intersection of the diagonals of the trapezoid are equal, that is, the triangles are equal.
Properties of a trapezoid extended to a triangle
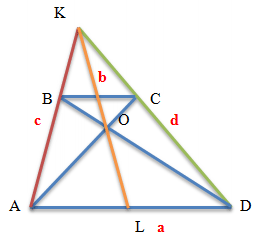
If the sides of the trapezoid are extended towards the smaller base, then the point of intersection of the sides
will coincide with a straight line that passes through the midpoints of the bases.
Thus, any trapezoid can be extended to a triangle.
Wherein:
- The triangles formed by the bases of a trapezoid with a common vertex at the point of intersection of the extended sides are similar
-
The straight line connecting the midpoints of the bases of the trapezoid is, at the same time, the median of the constructed triangle
Properties of a segment connecting the bases of a trapezoid
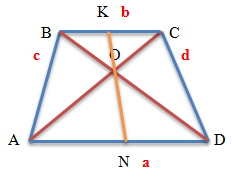
If you draw a segment whose ends lie on the bases of the trapezoid, which lies at the intersection point of the diagonals of the trapezoid (KN),
then the ratio of its constituent segments from the side of the base to the point of intersection of the diagonals (KO/ON)
will be equal to the ratio of the bases of the trapezoid (BC/AD).
KO/ON=BC/AD
This property follows from the similarity of the corresponding triangles (see above).
Properties of a segment parallel to the bases of a trapezoid
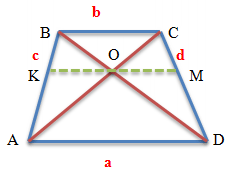
If you draw a segment parallel to the bases of the trapezoid and passing through the intersection point of the diagonals of the trapezoid,
then it will have the following properties:
- The specified segment (KM) is divided by the point of intersection of the diagonals of the trapezoid in half
-
The length of the segment passing through the point of intersection of the diagonals of the trapezoid and parallel to the bases is equal to KM = 2ab/(a + b)
Formulas for finding the diagonals of a trapezoid
The following are formulas that display the relationship between the sides, angles of a trapezoid and the size of its diagonals.
These formulas are useful for solving problems in geometry on the topic "trapezoid diagonals"
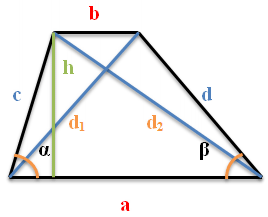
Further, the following notations are used in the formulas:
a, b - bases of the trapezoid
c, d - sides of the trapezoid
d1 d2 - trapezoid diagonals
α β - angles with a larger base of the trapezoid
Formulas for finding the diagonals of a trapezoid through the bases, sides and angles at the base

The first group of formulas (1-3) reflects one of the main properties of the trapezoid diagonals:
1. The sum of the squares of the diagonals of a trapezoid is equal to the sum of the squares of the sides plus twice the product of its bases. This property of the diagonals of a trapezoid can be proved as a separate theorem
2. This formula is obtained by converting the previous formula. The square of the second diagonal is thrown over the equal sign, after which the square root is extracted from the left and right sides of the expression.
3. This formula for finding the length of the diagonal of a trapezoid is similar to the previous one, with the difference that another diagonal is left on the left side of the expression
The next group of formulas (4-5) is similar in meaning and expresses a similar relationship.
The group of formulas (6-7) allows you to find the diagonal of a trapezoid if you know the larger base of the trapezoid, one side and the angle at the base.
Formulas for finding the diagonals of a trapezoid through the height
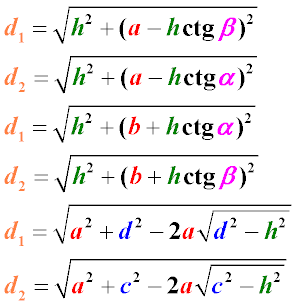
Note. In this lesson, the solution of problems in geometry about trapezoids is given.
If you have not found a solution to the geometry problem of the type you are interested in - ask a question on the forum.
A task.
The diagonals of the trapezoid ABCD (AD | | BC) intersect at point O.
Find the length of the base BC of the trapezoid if the base AD = 24 cm, length AO = 9 cm, length OS = 6 cm.
Solution.
The solution of this task is absolutely identical to the previous tasks in terms of ideology.
Triangles AOD and BOC are similar in three angles - AOD and BOC are vertical, and the remaining angles are pairwise equal,
since they are formed by the intersection of one line and two parallel lines.
Since the triangles are similar, then all their geometric dimensions are related to each other,
as the geometric dimensions of the segments AO and OC known to us by the condition of the problem.
That is
AO/OC=AD/BC
9 / 6 = 24 / B.C.
BC = 24 * 6 / 9 = 16
Answer: 16 cm
A task.
In the trapezoid ABCD it is known that AD=24, BC=8, AC=13, BD=5√17.
Find the area of the trapezoid.
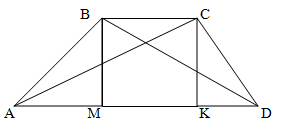
Solution.
To find the height of a trapezoid from the vertices of the smaller base B and C,
we lower two heights onto the larger base. Since the trapezoid is unequal, we denote the length AM = a, the length KD = b
(not to be confused with the notation in the formula for finding the area of a trapezoid).
Since the bases of the trapezoid are parallel and we have omitted two heights perpendicular to the larger base, then MBCK is a rectangle.
Means
AD = AM+BC+KD
a + 8 + b = 24
a = 16 - b
Triangles DBM and ACK are right-angled, so their right angles are formed by the heights of the trapezoid.
Let's denote the height of the trapezoid as h. Then by the Pythagorean theorem
h2 + (24 - a)2 = (5√17)2
and
h2 + (24 - b)2 = 132
We take into account that a = 16 - b,
then in the first equation
h2 + (24 - 16 + b)2 = 425
h2 = 425 - (8 + b)2
Substitute the value of the square of the height into the second equation, obtained by the Pythagorean Theorem.
We get:
425 - (8 + b)2 + (24 - b)2 = 169
-(64 + 16b + b)2 + (24 - b)2 = -256
-64 - 16b - b2 + 576 - 48b + b2 = -256
-64b = -768
b = 12
Thus, KD = 12
Where
h2 = 425 - (8 + b)2 = 425 - (8 + 12)2 = 25
h = 5
Find the area of a trapezoid using its height and half the sum of the bases
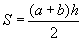 , where a b are the bases of the trapezoid, h is the height of the trapezoid , where a b are the bases of the trapezoid, h is the height of the trapezoid
S = (24 + 8) * 5 / 2 = 80 см2
Answer: The area of a trapezoid is 80 см2.
Trapeze (Trapezoid) |
Описание курса
| Right-Angled Trapezoid
|

