Problem 1

Condition: Ray KM intersects parallel planes α and β at points M₁ and M₂, and ray KP intersects them at points P₁ and P₂, respectively.
Calculate the length of segment M₁M₂ if:

• KM₁ = 8 cm

• M₁P₁ : M₂P₂ = 4 : 9

Solution: By making geometric constructions according to the problem's condition, we see that triangles KM₁P₁ and KM₂P₂ are formed.
They share a common angle K, and since planes α and β are parallel, lines M₁P₁ and M₂P₂ lying on these planes are also parallel.
Since parallel lines intersecting a third line form equal angles with it, triangles KM₁P₁ and KM₂P₂ are similar by three angles, meaning they have equal angles.

Since triangles KM₁P₁ and KM₂P₂ are similar, we have:

Let KM₂ be x. Thus:

Answer: 18 cm

Problem 2

Condition: Through point O, lying between parallel planes α and β, lines l and m are drawn. Line l intersects planes α and β at points A1 and A2,
respectively, and line m intersects them at points B1 and B2.
Find the length of segment A2B2 if A1B1 = 12 cm, and B1O : OV2 = 3 : 4.

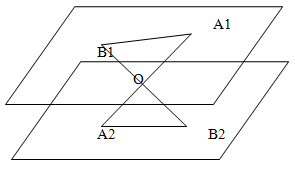
Solution: Through lines A1A2 and B1B2, we can draw a plane that intersects the parallel planes along parallel lines A1B1 and A2B2.
In the formed triangles OA1B1 and OA2B2, the corresponding angles are equal. The angles at vertex O are equal as vertical angles,
and the others are equal as alternate interior angles at parallel lines. Therefore, triangles OA1B1 and OA2B2 are similar.

In similar triangles, the corresponding sides are proportional to the similarity coefficient.

Thus:

Therefore:

Answer: 16 cm