Central and Axial Symmetry

Definition

Symmetry (meaning "correspondence") refers to the properties of geometric objects to combine with each other under certain transformations. Symmetry
is understood as any regularity in the internal structure of a body or figure. Symmetry relative to a point is called central symmetry, and symmetry relative
to a line is called axial symmetry.

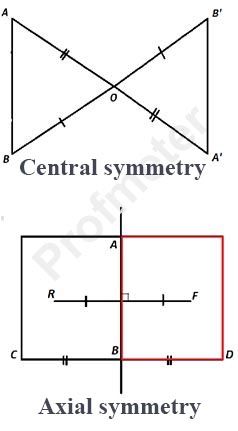
Central Symmetry

Symmetry relative to a point implies that on both sides of the point at equal distances, there are corresponding elements, such as other points or loci
of points (straight lines, curved lines, geometric figures). If you connect symmetrical points (points of a geometric figure) with a line through the point
of symmetry, then the symmetrical points will lie at the ends of the line, and the point of symmetry will be its midpoint. If you fix a point of symmetry
and rotate the line, then the symmetrical points will describe curves, each point of which will also be symmetrical to a point on another curved line.

Axial Symmetry

Symmetry with respect to a line (axis of symmetry) assumes that along a perpendicular drawn through each point of the axis of symmetry, two symmetrical
points are located at the same distance from it. The same geometric figures can be located with respect to the axis of symmetry (line) as with respect to
the point of symmetry.

An example is a notebook sheet that is bent in half if a straight line (axis of symmetry) is drawn along the fold line. Each point of one half of the sheet will
have a symmetrical point on the other half of the sheet if they are located at the same distance from the fold line perpendicular to the axis.

The line of axial symmetry, as in the figure, is vertical, and the horizontal edges of the sheet are perpendicular to it. That is, the axis of symmetry serves
as a perpendicular to the midpoints of the horizontal lines bounding the sheet. Symmetric points (R and F, C and D) are located at the same distance from
the axial line - the perpendicular to the lines connecting these points. Therefore, all points of the perpendicular (axis of symmetry) drawn through the middle
of the segment are equidistant from its ends; or any point of the perpendicular (axis of symmetry) to the middle of the segment is equidistant from the ends
of this segment.

Additional Information

1. Applications in Nature and Art: Symmetry is prevalent in nature and art. For example, many flowers exhibit radial symmetry, and human faces
   often show bilateral symmetry. Artists and architects use symmetry to create aesthetically pleasing designs.

2. Mathematical Representation: In mathematics, symmetry can be represented using transformations such as reflections, rotations, and translations.
   These transformations help in understanding the properties of geometric figures and solving problems related to symmetry.

3. Symmetry in Physics: Symmetry principles are fundamental in physics. They help in understanding the laws of nature, such as conservation laws.
   For instance, the conservation of momentum is related to the symmetry of space.

4. Symmetry in Chemistry: Molecules often exhibit symmetry, which affects their chemical properties and reactions. The study of molecular symmetry
   is essential in understanding the behavior of molecules in different chemical processes.