See also sine of some angles (sin 60, sin 30, sin 45).

Sine of an angle

For the right-angled triangle ABC, the sine (sin) of the angle A is the aspect ratio of BC and AB.

The sine of the angle of a right triangle is equal to the ratio of the opposing leg to the hypotenuse.

sin A = BC / AB

The value of the sine function of the alpha angle in a right-angled triangle will always be the same for the same angle, regardless of the dimensions of the sides of the triangle.

The sine function of the angle (sin)

SINUS (sin) is a trigonometric quantity, a function of the angle that varies with the angle. "Sinus" is translated from Latin as "bend", "curvature".

Moving the moving radius in a full circle counter-clockwise, we get positive angles from 0 ° to 360 °.

Moving the moving radius along the full circle in a clockwise direction, negative angles are obtained, respectively from 0 ° to -360 °.

In a right-angled triangle, the side opposite the right angle is called the hypotenuse, and the other sides by the legs.

The sine of an acute angle in a right-angled triangle is the ratio of the opposing leg to the hypotenuse.

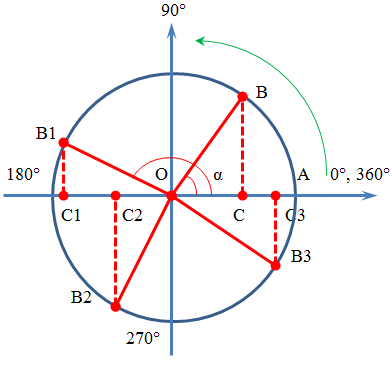
Consider on the circle the changes in the sine function of the acute angle, constructing on the fixed side of the corner (OA) the rectangle of the right triangle (OC), whose hypotenuse has a moving radius (OB) (Fig. 1).

By the definition of the sine of the angle: sin⁡ a = BC / OB.

For the unit circle, where OB = 1, this is the length of the segment BC. Consequently, the sine of an angle is the magnitude of the projection of the movable segment OB on the y-axis.

Consider changes in the function sin α (segment BC) when the moving radius moves along the circumference and the angle increases. The limits of the change in the sine of the angle will be determined from the quadrants.

In the 1st quadrant ( ВС ):

for α = 0º sin α = 0;

for 0º < α < 90º 0 < sin α < 1;

for α = 90º sin α = 1.

In the 2nd quadrant ( В₁С₁ ):

for α = 90º sin α = 1;

for 90º < α < 180º 1 > sin α > 0;

for α = 180º sin α = 0.

For the first half-circle passed, sin α changes from 0 to 0, and its largest value equal to 1 coincides with the length of the radius on the positive y-axis.

The second half-circle of the moving radius movement can be considered as a positive direction (when moving the OBs further counter-clockwise) and as a negative direction (if the OB rotate clockwise). Let us consider only the positive direction.

In the third quadrant ( В₂С₂ ):

for α = 180º sin α = 0;

for 180º < α < 270º 0 > sin α > -1;

for α = 270º sin α = -1;

In the IV quadrant ( В₃С₃ ):

for α = 270º sin α = -1;

for 270º < α < 360º -1 < sin α < 0;

for α = 360º sin α = 0.

For the passed second semicircle, sin α changed from 0 to 0, and its smallest value, equal to -1, coincides with the length of the radius, but the negative semiaxis y.

For the entire rotation of the moving radius OB, from coincidence with OA to their second coincidence, the angle has numerically changed from 0º to 360º, and the numerical value of the sine of the angle varied from 1 to -1.см. также - таблица значений основных углов тригонометрических функций.