SEGMENT

A segment is a part of a line that consists of all the points of this line that lie between two given points. These given points are called the ends
of the segment and are used to designate it (Fig. 1).

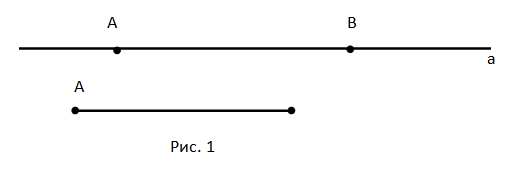
A Segment and Points that Belong and Do Not Belong to a Segment

A segment AB lies on a line a; it is designated as follows: AB ∈ a. It is bounded by the starting point of the segment (point A) and
the end point of the segment (point B).

Intersection of Lines

When two lines intersect at one point, they form four angles. In this case, they are vertical and adjacent in pairs.

• Vertical angles are angles that are formed by the intersection of two lines and are not adjacent. They have a common vertex and are equal
  to each other.

• Adjacent angles are angles formed by the intersection of two lines that have a common side, a common vertex, and complement each other
  to 180 degrees. The other two sides form a straight line. The sum of adjacent angles is 180 degrees.

Additional Information

1. Points: A point is a basic concept in geometry that has no size, shape, or other characteristics other than its position. Points are denoted by
   capital letters of the Latin alphabet (e.g., A, B, C).

2. Lines: A line is an infinite one-dimensional figure consisting of an infinite number of points located in one direction. Lines are denoted by
   lowercase letters of the Latin alphabet (e.g., a, b, c) or by two points lying on this line (e.g., AB).

3. Segments: A line segment is a part of a line bounded by two points. The length of a line segment is the distance between its endpoints. Line
   segments are denoted by two capital letters representing its ends (e.g., AB).

4. Practical Application: Understanding points, line segments, and lines is important for solving various problems in geometry, such as constructing
   figures, calculating distances and angles, and for applications in engineering and architecture.

5. Properties of Segments:

   • A segment has a definite length, which can be measured.

   • A segment can be divided into several parts, each of which is also a segment.

   • A segment can be extended in both directions to form a line.

6. Use in Problems: Segments are often used in construction problems where it is necessary to find specific points, lengths, or angles.
   For example, in problems involving dividing a segment in a given ratio or finding the midpoint of a segment.