Tangent

Basic Concepts, Properties, and Formulas

The trigonometric function tangent of an angle is denoted as tan. The word "tangent" literally translates from Latin as "touching."

The tangent of an acute angle in a right triangle is the ratio of the length of the opposite leg to the length of the adjacent leg.

For visual memory: In the diagram below, the necessary sides of the triangle are marked with a double-sided arrow.
The "blue" leg should be divided by the "red" leg.

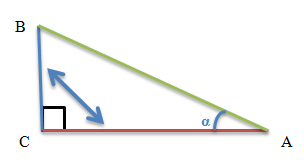
Graphical Representation of the Tangent Function

In simple terms, to calculate the tangent of an angle in a right triangle, we proceed as follows:

1. Take the length of the leg opposite the acute angle α - this is the leg BC, marked in blue in the diagram.
2. Divide it by the length of the other leg (this is the leg AC, marked in red in the diagram).
3. The resulting value will be correct and the same for this angle in any right triangle and will not depend on the size of the triangle.

From this, it follows that:

• Knowing the lengths of the legs in a right triangle, you can determine the value of the tangent of the angle, and then, using the
  arctangent function (arctan⁡), you can determine the measure of this angle.
• Since tan⁡ α  is always equal to tan ⁡α= BC / AC, if the measure of the angle α\alpha and one of the legs are known, you can always
  calculate the length of the other leg

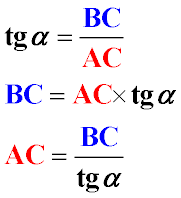
Formula for Finding the Tangent in a Right Triangle and the Sides of the Triangle through the Tangent

The relationships described above are often used in problem-solving. It is implied that by using the basic property of the tangent function
tan ⁡α = BC / AC (see the diagram with side designations above), you can easily find the dimensions of the triangle or another geometric figure.
However, in practice, this simplest property of the tangent often causes difficulties in solving problems.

Trigonometric Circle of Tangent

The change in the value of the tangent function depending on the angle, including for positive and negative angles.

The tangent line is the tangent ll to the unit circle at point A (1;0). The positive direction of the tangent line is taken from bottom to top.

By the definition of the tangent of an angle ( tan⁡ α = sin ⁡α / cos ⁡α), tan ⁡α=BA1 / OA1 = CA / OA = CA, since OA=1.
That is, the tangent of the angle α is the length of the segment AC on the tangent line. In other words, the tangent of an angle is the length
of the tangent segment drawn through point A (the end of the fixed radius), from the point of tangency A to the intersection with the extension
of the movable radius OB.

Let's consider the change in the length of the segment AC as the movable radius OB moves along the circle and the angle increases.

Note that the values coincide in the first and third quadrants, and in the second and fourth quadrants:

Values of the Tangent Function of an Angle (tan⁡α\tan \alpha)

Refer to the link if you need to find the exact trigonometric values of the tangent of commonly encountered angles.

In the table below, information is provided on whether the value of the tangent function is positive or negative for all angles from 0 to 360 degrees
(which corresponds to values from 0 to 2π radians). For easier visual memory, where the tangent function takes positive values, tan ⁡α is marked in red,
and where negative - in blue.

See Also:

• Explanation of how the tangent of 45 degrees (tan⁡45) was calculated.
• Explanation of how the tangent of 30 degrees (tan⁡30) was calculated.
• Explanation of how the tangent of 60 degrees (tan⁡60) was calculated.