|
|
A hexagon is a polygon whose total number of angles (vertices) is six.
Convex Hexagon
A convex hexagon is a polygon with six vertices, where all points of the hexagon lie on one side
of a line drawn between any two of its adjacent vertices.
Sum of the Interior Angles
The sum of the interior angles of a convex hexagon can be determined using the general formula
for the sum of the interior angles of an ( n )-sided polygon, which is
180° * (n - 2) .
For a hexagon ( n = 6 ):
180° * (6 - 2) = 720°
This means the sum of the interior angles of a convex hexagon is 720 degrees.
Finding the Area of an Irregular Hexagon
When solving problems to find the area of an arbitrary (irregular) hexagon, the trapezoid method is often used.
This method involves dividing the hexagon into separate trapezoids, the area of each of which can be calculated
using well-known formulas.
Regular Hexagon
A regular hexagon is a hexagon where all sides and all interior angles are equal.
Properties of a Regular Hexagon
- Equal Interior Angles: All interior angles are equal to each other. Each interior angle of a regular hexagon is ( 120° ).
- Equal Sides: All sides are equal in length.
- Circumscribed Circle: The length of each side of a regular hexagon is equal to the radius of the circumscribed circle
(the circle that passes through all vertices of the hexagon).
- Inscribed Circle: A regular hexagon can also have an inscribed circle (a circle that is tangent to all sides of the hexagon).
- Tiling the Plane: A regular hexagon can fill the plane without gaps or overlaps, making it useful in tiling patterns.
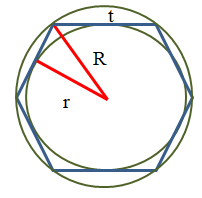
Formulas for a regular hexagon
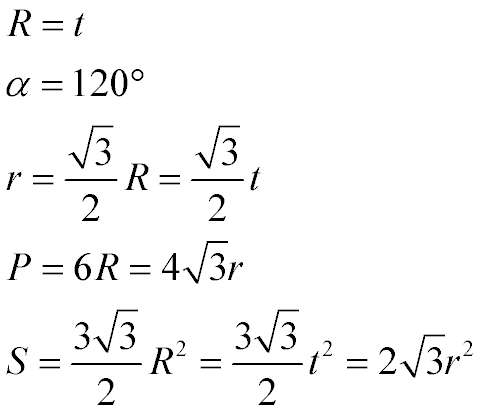
(in the order of the formulas)
- The radius of the circumscribed circle (R) of a regular hexagon is equal to its side (t)
-
All interior angles are equal to 120 degrees
-
The radius of the inscribed circle (r) is equal to the root of three, divided by two and multiplied by the length of the side t
(radius of the circumscribed circle R)
-
The perimeter of a regular hexagon (P) is equal to six radii of the circumscribed circle (R) or four roots of three,
multiplied by the radius of the inscribed circle (r)
-
The area of a regular hexagon is equal to three roots of three divided by two, multiplied by the square of the radius
of the circumscribed circle (R) or the square of the side (t); or the area of a regular hexagon is equal to two roots of three,
multiplied by the square of the radius of the inscribed circle (t)
Problem
Find the volume of a cylinder inscribed in a regular hexagonal prism, each edge of which is equal to ( t ).
Solution
-
Height of the Cylinder: Since the cylinder is inscribed in the hexagonal prism, the height of the cylinder ( H )
is equal to the height of the prism. Given that the height ( a ) is equal to the edge length ( t ), we have ( H = t ).
-
Radius of the Base of the Cylinder: The radius of the base of the cylinder is equal to the radius of the circle inscribed
in the regular hexagon. For a regular hexagon with side length ( t ), the radius ( R ) of the inscribed circle (also known
as the apothem) is: R = t √3 / 2
-
Volume of the Cylinder: The volume ( V ) of a cylinder is given by the formula:
V = π r2 H
Substituting the values of ( r ) and ( H ):
V = π ( ( t √3 / 2 )2 t
Simplifying the expression:
V = π ( ( 3 t2 / 4 ) t
V = 3 π t3 / 4
So, the volume of the cylinder is indeed: V = 3 π t3 / 4

Explanation
- Height of the Cylinder: The height of the cylinder is the same as the height of the hexagonal prism, which is given as ( a ).
- Radius of the Base: The radius of the inscribed circle in a regular hexagon with side length ( t ) is R = t √3 / 2.
This is because the apothem of a regular hexagon is the distance from the center to the midpoint of any side,
forming a 30-60-90 triangle.
- Volume Calculation: Using the formula for the volume of a cylinder, we substitute the radius and height to find the volume.
Polygons |
Описание курса
| Sum of the angles of a polygon
|

