Angle Bisector of a Triangle

An angle bisector of a triangle is a segment of the angle bisector that connects the vertex of the angle with a point on the opposite side.

Triangle angle bisectors have many properties that are described through the properties of a triangle. Understanding these properties can help in solving
geometric problems.

Properties of Triangle Bisectors

1. Angle Division: A triangle bisector drawn from a given vertex is identical to the bisector of the corresponding angle. It divides the angle of the
   triangle in half.

2. Intersection Point: All three triangle bisectors intersect at one point, which is always located in the plane of the triangle and is the center of
   the inscribed circle. This refers to the bisectors of the interior angles of the triangle.
   

3. Ratio of Segments: Each bisector of a triangle is divided by the intersection point of the bisectors in the ratio of the sum of the adjacent sides
   to the opposite side, counting from the vertex.
   

4. Proportional Division: The bisector of any interior angle of a triangle divides the opposite side into parts proportional to the sides of the triangle.

5. Exscribed Circles: The bisectors of one interior and two exterior angles of a triangle intersect at one point. This point is the center of one of the
   three exscribed circles of the triangle.

6. Perpendicularity: The angle between the bisectors of two adjacent angles (between the internal and external bisectors of the angles of a triangle
   at the same vertex) is 90 degrees.
   

Properties of the Bisectors of an Isosceles Triangle

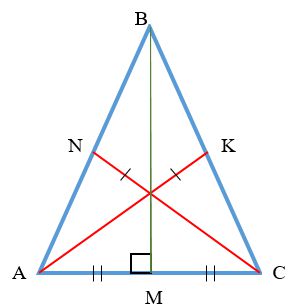
1. Coincidence of Lines: In an isosceles triangle, the median, bisector, and altitude drawn to the base of the triangle are the same.

2. Steiner-Lemus Theorem: If two bisectors in a triangle are equal, then the triangle is isosceles, and the third bisector is simultaneously
   the median and the altitude of the angle from which it emerges.

3. Equality of Bisectors: In an isosceles triangle, two bisectors are equal, and the third bisector is its median and altitude.
   

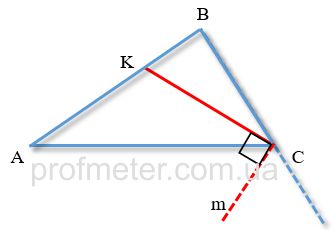
4. Parallel Bisector: One and only one bisector of the external angle of a non-equilateral triangle can be parallel to the opposite side (the base)
   if the triangle is isosceles.

Properties of the Bisectors of an Equilateral Triangle

1. Parallel Bisectors: In an equilateral triangle, all three bisectors of the external angles are parallel to the opposite sides.

2. Equality of Internal Bisectors: In an equilateral triangle, all three internal bisectors are equal.

3. Coincidence of Remarkable Lines: In an equilateral triangle, all three "remarkable" lines (altitude, bisector, and median) coincide, and three
   "remarkable" points (the orthocenter, the centroid, and the centers of the inscribed and circumscribed circles) are at one point of intersection
   of the "remarkable" lines, i.e., they also coincide.

Formulas for Finding the Bisector of an Angle

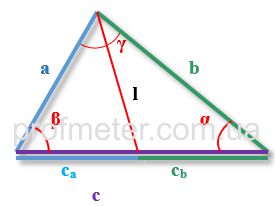
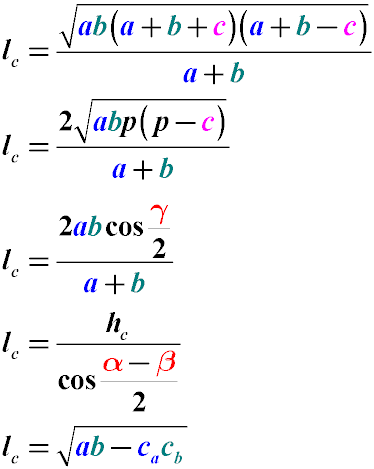
To find the length of the bisector of an angle in a triangle, we use the following notation:

• a, b, c - sides of a triangle, with the bisector drawn from the angle located between sides aa and bb

• α,β,γ - angles of a triangle opposite sides a,b,ca, b, c respectively

• p - semiperimeter of a triangle (half the sum of all its sides)

• c_a,c_b - segments into which the bisector drawn from angle γ\gamma divides side cc

• l_c - length of the bisector drawn to side cc from angle γ\gamma

The length of the bisector l_c also can be found using the formula:

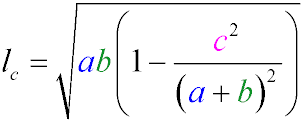
Formulas for Finding the Distance from an Angle to the Intersection Point of the Bisectors

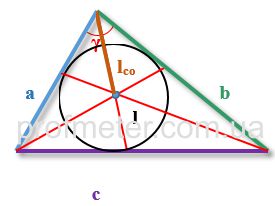
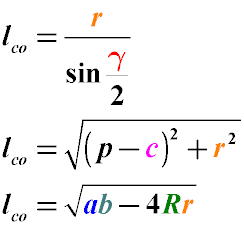
To find the distance from an angle to the intersection point of the bisectors, we use the following notation:

• l_co - length of the segment lying on the bisector from the vertex of the angle to the center of intersection of the bisectors

• r - radius of the circle inscribed in the triangle

• R - radius of the circumscribed circle

• a, b, c - sides of the triangle, with the bisector drawn from the angle located between the sides aa and bb

• γ - angle of the triangle opposite the side cc

• p - semiperimeter of the triangle (half the sum of all its sides)

The relationship between the length of a segment of the bisector to the center of intersection of the bisectors, the radii of the inscribed and
circumscribed circles, and the lengths of the sides of the triangle can be described using specific geometric formulas.

Problem

Ray AD is the bisector of angle A. Points B and C are marked on the sides of angle A so that ∠ADC=∠ADB.

Prove that AB=AC.

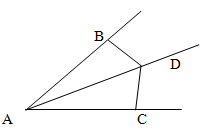
Solution

Given Information:

AD is the bisector of ∠A.
∠ADC=∠ADB.

1. Triangles △ADC and △ADB: Consider the triangles △ADC and △ADB.

2. Angle-Side-Angle (ASA) Congruence:

   • ∠CAD=∠BAD (since AD is the bisector of ∠A)

   • ∠ADC=∠ADB (given)

   • AD is common to both triangles

   By the ASA congruence criterion, we have:

Corresponding Parts of Congruent Triangles (CPCTC):

Since △ADC≅△ADB, their corresponding sides are equal:

Conclusion

We have proven that AB=AC based on the properties of the bisector and the congruence of triangles.