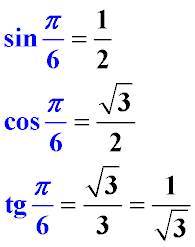Note. See also a table of values for trigonometric functions for popular angles.
Sine 30, cosine 30, tangent 30 degrees - table of values
value of the angle α
(degrees)
|
value of the angle α
in radians
(through the number of pi)
|
sin
(sine)
|
cos
(cosine)
|
tg
(tangent)
|
ctg
(cotangent)
|
sec
(secant)
|
cosec
(cosecant)
|
|
30
|
π/6
|
1/2
|
√3/2
|
1/√3
|
√3
|
2/√3
|
2
|
How were the values of the sine, cosine and tangent of 30 degrees calculated?
The following is a step-by-step explanation of the logic for calculating data values for an angle of thirty degrees. To achieve this arbitrary construction of right triangle with respective angles and calculated values of sine, cosine and tangent of 30 degrees.
The value of trigonometric functions of the sinus, cosine, tangent at α = 30°
Consider the algebraic triangle ABC. Let each of his sides will be equal to a. According to the properties of an equilateral triangle, all its angles are equal, including the angle ∠B = 60 °.
First we will make additional construction. From the top of A to the BC side we will carry out the median AO.
Median AO in an equilateral triangle is simultaneously bisector and height.
Then the rectangle AOB is a rectangular with an angle ∠BAO = 30 °. (Angle B is equal to 60 degrees ∠BOA is straight and equal to 90 degrees, so ∠BAO = 180 - 90 - 60 = 30 degrees)
We can calculate the sine, cosine, and tangent values if we find the correlation of the corresponding sides for a 30-degree angle in a rectangular triangle. Since the values of these trigonometric functions depend exclusively on the degree angle of the angle, the correlation we calculate will be the values of the sinus 30, cosine 30, and the tangent 30 degrees.

For a given rectangular triangle we calculate the value of the trigonometric functions of its angles. Let's do it first for an angle of 30 degrees.
The size of the hypotenuse is known to us and equal to a. The OB leg is equal to a / 2, since AO is the median of the triangle ABC. We will find a leg AT.
By Pythagoras's theorem:
АВ2=АО2+ОВ2;
АО2=АВ2-ОВ2
substitute in the resulting equation the value of the hypotenuse (we assume that it is equal to a)
АО2=a2- (а/2)2
АО2=3a2/4
AO=√( 3a2/4 ) =a√3/2
Now we have computed all the sides of the rectangular triangle ABO. Taking into account that AB = a, OB = a / 2, AO = a√3 / 2, we will calculate the obtained values from the relations of the sides of the rectangular triangle. According to the definition of a sinus, a cosine and a tangent:
sin 30 = OB / AB (by definition of sinus - the ratio of the opposing leg to the hypotenuse)
cos 30 = AO / AB (by cosine definition - the ratio of the adjacent leg to the hypotenuse)
tg 30 = OB / AO (by the definition of the tangent - the relation of the opposing leg to the adjoining one)
Reports have:
Given that the triangle ABC is uniform, then BO is AB / 2, and the value of AO is calculated above. As a result, we get tabular values of sin 30, cos 30 and tg 30 degrees
Table values for sin 30, cos 30 and tg 30 degrees:


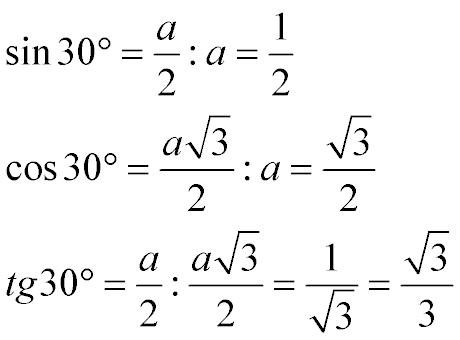
That is:
The tangent of 30 degrees is equal to the root of three to three
A sinus of 30 degrees is equal to one second or 0.5
The cosine is 30 degrees equal to the root of three to two
Sine, cosine and tangent angle π / 6
Proceeding from the above-stated principle of translating the radian in degrees, angle of pi / 6 equal
180 / 6 = 30 degrees.
For a more convenient visual perception, these values are shown below in the figure