Equation of a Circle

Analytical geometry provides methods for solving geometric problems by referring all given and sought points and lines to the same coordinate system.

In a coordinate system, each point can be characterized by its coordinates, and each line by an equation with two unknowns, the graph of which
represents this line. Thus, a geometric problem is reduced to an algebraic one, where all calculation techniques are well-developed.

A circle is a geometric locus of points with one specific property: each point of the circle is equidistant from one point, which is called the center.
The equation of a circle must reflect this property and satisfy this condition.

The geometric interpretation of the equation of a circle is the set of all points that form the circle.

Equation of a Circle in Cartesian Coordinates

If we place a circle in a coordinate system, then all points of the circle meet one condition: the distance from them to the center of the circle must
be the same.

Consider a circle with a center at point A and a radius R placed in the coordinate plane.

If the coordinates of the center are (a,b), and the coordinates of any point on the circle are (x, y), then the equation of the circle has the form:

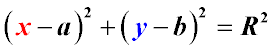
This is the equation of a circle in Cartesian coordinates when the center of the circle does not coincide with the origin.

If the center of the circle coincides with the origin (0,0)(0, 0), then the equation simplifies to:

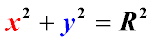
This equation states that the square of the radius of the circle is equal to the sum of the squares of the coordinates of any point on the circle.

Explanation and Examples

1. Circle with Center at the Origin:
   • Equation: x²+y²=R²
   • Example: For a circle with radius 5, the equation is x²+y²=25.

2. Circle with Center Not at the Origin:

   • Equation: (x−a)²+(y−b)²=R²
   • Example: For a circle with center at (3, 4) and radius 5, the equation is (x−3)²+(y−4)²=25.

Applications

1. Geometric Problems: The equation of a circle is used to solve various geometric problems, such as finding the intersection points
   of circles and lines, determining the tangents to a circle, and calculating the area and circumference of a circle.
2. Physics and Engineering: Circles are fundamental in physics and engineering, where they are used to model circular motion, design
   gears and wheels, and analyze wave patterns.
3. Computer Graphics: In computer graphics, the equation of a circle is used to draw circles and arcs, create animations, and simulate
   physical phenomena.

Conclusion

Any geometric figure for which the locus of points is determined by an equation that connects the coordinates of its points can be analyzed
using analytical geometry. Conversely, an equation relating the coordinates xx and yy defines a line or curve as the locus of points in a plane
whose coordinates satisfy the given equation.

Examples of solving problems about the equation of a circle

Task

Write the equation of a circle with center at point O(2,−3) and radius 4.

Solution

The general equation of a circle in Cartesian coordinates is given by:

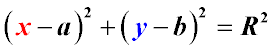
where (a,b) are the coordinates of the center of the circle and R is the radius.

Given:

• Center O(2,−3)
• Radius R=4

Substitute the given values into the general equation:

Simplify the equation:

Answer

The equation of the circle with center at point O(2,−3) and radius 4 is:

Task: Does the point of the equation of the circle belong to

Solution

To determine if the point A(2,3) lies on the circle, we need to substitute the coordinates of the point into the equation of the circle and see
if the equation holds true.

The equation of the circle is:

Substitute the coordinates of point A(2,3) into the equation:

Simplify the expression:

Since the left-hand side of the equation (36) does not equal the right-hand side (16), the point A(2,3)A(2, 3) does not satisfy the equation
of the circle.

Answer

The point A(2,3) does not belong to the equation of the circle (x−2)²+(y+3)²=16.