Table of values for trigonometric functions

Note. In this table of values of trigonometric functions, the √ sign for the square root is used. To indicate the fraction - the symbol "/".

See also useful materials:

• The transformation formulas for trigonometric functions 
• Table derivative of trigonometric functions 
• How these values are calculated 

To determine the value of the trigonometric function, find it at the intersection of the line indicating the trigonometric function. For example, a sine of 30 degrees - we look for a column with the heading sin (sinus) and find the intersection of this column of the table with the line "30 degrees", at their intersection we read the result - one second. Similarly, we find the cosine of 60 degrees, the sine of 60 degrees (once again, in the intersection of the column sin (sinus) and the line of 60 degrees we find the value sin 60 = √3 / 2), etc. Similarly, the values ​​of the sines, cosines and tangents of other "popular" angles are found.

Sinus pi, cosine pi, tangent of pi and other angles in radians

The following table of cosines, sines and tangents is also suitable for finding the value of trigonometric functions, the argument of which is given in radians. To do this, use the second column of the angle values. Due to this, it is possible to translate the value of popular corners from degrees to radians. For example, find the angle of 60 degrees in the first line and below it read its value in radians. 60 degrees is equal to π / 3 radians.

The number pi uniquely expresses the dependence of the length of the circle on the degree measure of the angle. Thus, the pi of the radians is 180 degrees. 

Any number expressed in terms of pi (radian) can easily be converted to a degree measure, replacing the number pi (π) by 180.

Examples:

1. The Sine of pi.
sin π = sin 180 = 0
Thus, the sine pi is the same as the sine of 180 degrees and it is zero.

2. The cosine of pi.
cos π = cos 180 = -1
Thus, the cosine of pi is the same as the cosine of 180 degrees and it is equal to minus one.

3. The tangent of pi
tg π = tg 180 = 0
Thus, the tangent pi is the same as the tangent of 180 degrees and it is zero.

Table of values of the sine, cosine, tangent for angles 0 - 360 degrees (often occurring values)  

the value of angle α (degrees)	the value of angle α in radians (Via pi)	sin  (sine)	cos  (cosine)	tg  (tangent)	ctg  (cotangent)	sec  (secant)	cosec  (cosecant)
0	0	0	1	0	-	1	-
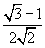
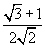
15	π/12			2 - √3	2 + √3
30	π/6	1/2	√3/2	1/√3	√3	2/√3	2
45	π/4	√2/2	√2/2	1	1	√2	√2
60	π/3	√3/2	1/2	√3	1/√3	2	2/√3
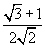
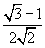
75	5π/12			2 + √3	2 - √3
90	π/2	1	0	-	0	-	1
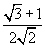
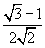
105	7π/12		-	- 2 - √3	√3 - 2
120	2π/3	√3/2	-1/2	-√3	-√3/3
135	3π/4	√2/2	-√2/2	-1	-1	-√2	√2
150	5π/6	1/2	-√3/2	-√3/3	-√3
180	π	0	-1	0	-	-1	-
210	7π/6	-1/2	-√3/2	√3/3	√3
240	4π/3	-√3/2	-1/2	√3	√3/3
270	3π/2	-1	0	-	0	-	-1
360	2π	0	1	0	-	1	-

If in the table of values ​​of trigonometric functions a dash (tangent (tg) 90 degrees, cotangent (180 degrees)) is specified instead of the function value means that for a given value of the degree measure of the angle the function has no definite value. If there is no dash, the cage is empty, so we have not yet made the desired value. We are interested in what queries users come to us and add new values ​​to the table, despite the fact that current data on the values ​​of cosines, sines and tangents of the most frequently encountered angles is enough to solve most problems.

Table of values of trigonometric functions sin, cos, tg for the most popular angles 
0, 15, 30, 45, 60, 90 ... 360 degrees

value of angle α (degrees)	value of angle α in radians	sin (sine)	cos (cosine)	tg (tangent)	ctg (cotangent)
0	0	0	1	0	-
15	π/12	0,2588	0,9659	0,2679	3,7321
30	π/6	0,5000	0,8660	0,5774	1,7321
45	π/4	0,7071	0,7071	1	1
50	5π/18	0,7660	0,6428	1.1918	0,8391
60	π/3	0,8660	0,5000	1,7321	0,5774
65	13π/36	0,9063	0,4226	2,1445	0,4663
70	7π/18	0,9397	0,3420	2,7475	0,3640
75	5π/12	0,9659	0,2588	3,7321	0,2679
90	π/2	1	0	-	0
105	5π/12	0,9659	-0,2588	-3,7321	-0,2679
120	2π/3	0,8660	-0,5000	-1,7321	-0,5774
135	3π/4	0,7071	-0,7071	-1	-1
140	7π/9	0,6428	-0,7660	-0,8391	-1,1918
150	5π/6	0,5000	-0,8660	-0,5774	-1,7321
180	π	0	-1	0	-
270	3π/2	-1	0	-	0
360	2π	0	1	0	-

Sometimes for fast calculations you need not an exact, but a calculated value (the number of decimal fractions). Therefore, in addition to the table of exact values of trigonometric functions, the same values are given, but in the form of a decimal fraction rounded to the fourth digit. In addition, the table includes "non-standard" values of tangent, cosine, sine 140 degrees, sine 105, 70, cosine 105 and 50 degrees.

Example: a 60-degree sine is approximately 0.866025404, and the table shows a value of sin 60 ≈ 0.8660; The cosine of 30 degrees is equal to the same number(see. formulas for transforming trigonometric functions)