Median of a Triangle

The word "median" is translated as "equidistant side." To construct a median, you need to connect the middle
of the side of the triangle with a segment to the opposite vertex of the triangle. The resulting segment is the median
of the triangle.

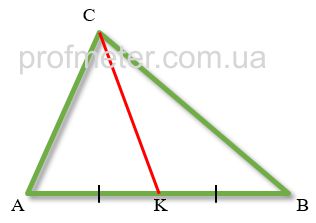
Definition

The median of a triangle is a segment drawn from the vertex of the triangle, connecting this vertex with the middle of
the opposite side of the triangle.

In the figure, the median CK is marked in red. At the same time, it divides the side AB of the triangle in half, so AK=KB.

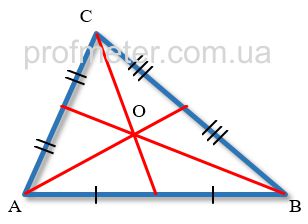
Properties of the Median

1. Intersection Point: All medians of a triangle intersect at one point located in the plane of the triangle, which is
   its center of gravity (centroid).

2. Centroid: The centroid is the point of intersection of the medians and is located 2/3 of the distance from each
   vertex along the median.

3. Equal Area: The median divides the triangle into two equal (in area) triangles.

4. Six Equal Triangles: The triangle is divided by three medians into six equal triangles.

5. Triangle Inequalities: The lengths of the medians satisfy the triangle inequalities.

6. Right Triangle: In a right triangle, the median drawn from the vertex with a right angle is equal to half
   the hypotenuse.

7. Isosceles Triangle: In an isosceles triangle, the median, bisector, and altitude drawn to the base of
   the triangle coincide.

8. Equilateral Triangle: In an equilateral triangle, all three lines (altitude, bisector, and median) coincide,
   and the three points (the orthocenter, centroid, and center of the inscribed and circumcircles) are at the same
   intersection point.

Midline of a Triangle

The segment drawn through the bases of any two medians of a triangle is its midline. 

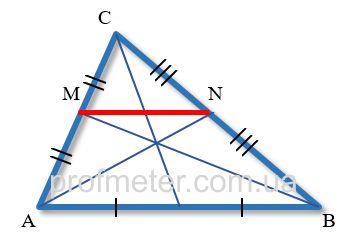
The midline of a triangle connects two points of the ends of the medians lying on the sides of the triangle.
The midline is always parallel to the side of the triangle with which it has no common points and is equal to half
the length of that side.

Formulas for the Median of an Arbitrary Triangle

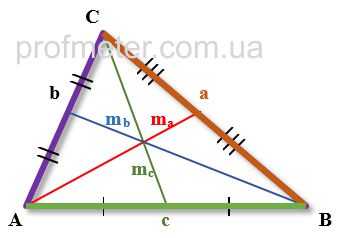
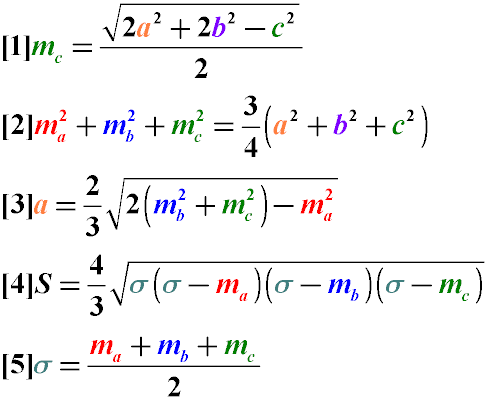
• The length of the median drawn to a side of an arbitrary triangle is equal to half the square root of twice the sum
  of the squares of the other two sides minus the square of the side to which the median is drawn (Formula 1)
• The sum of the squares of the medians of a triangle is equal to 3/4 of the sum of the squares of its sides (Formula 2)
• The length of a side of a triangle is equal to 2/3 of the square root of twice the sum of the squares of the medians
  drawn to its other two sides minus the square of the median drawn to the desired side (Formula 3)
• The area of ​​a triangle can be found from the lengths of its medians, using the value of the half-sum of the lengths
  of the medians (Formulas 4 and 5)