Описание курса Axioms of planimetry Axiom of the affiliation of points and lines The axiom of the arrangement of points on the line The axiom about the length of the segments The existence of a triangle equal to a given Points, segments and straight lines Central and axial symmetry Angle. Angles on the plane Angle Bisector Angle Bisector of a Triangle Circle. Equation of a circle Chord Triangle Median of a triangle Median of a right triangle How to find the median length of a triangle Finding area using medians Height of a Triangle Area of ​​a triangle Problems on finding the area of ​​an arbitrary triangle Right Triangle Hypotenuse of a right triangle Isosceles triangle Quadrilateral (quadrangle) Existence of a quadrilateral with given sides Parallelogram Height of parallelogram Trapeze (Trapezoid) Diagonals of a trapezoid Right-Angled Trapezoid Polygons Hexagon and its properties Trigonometry Sine The sine theorem Tangent and its properties Table of values for trigonometric functions Sine, to the sine, the tangent of the angle of 15 degrees (sin 15 cos 15 tg 15) Sine, cosine and tangent angles of 30 degrees (sin cos tg 30) - table of values Sine, cosine, tangent angle of 45 degrees (sin 45, cos 45, tg 45) Sine, cosine, tangent of angle 30 and 60 degrees (sin cos tg 30 and 60) Sine, cosine, tangent angle of 105 degrees (sin 105 cos 105 tg 105) Sine, to the sine, the tangent of the angle is 120 degrees (sin 120 cos 120 tg 120) Trigonometric identities and transformations Cosine of a double angle Trigonometric Circle Stereometry Pyramid. Problem solving Regular pyramid Regular pyramid with a quadrilateral base Problems about a regular quadrangular pyramid Finding the angles of a regular quadrangular pyramid With a triangle at the base Regular triangular pyramid (regular pyramid with a triangle at the base) Regular tetrahedron Pyramid with a right triangle at the base Prism. Parallelepiped. Cube. Solving problems Volume of a Prism Triangular Prism (with a Triangle at the Base) Volume of a Regular Triangular Prism Volume of a Prism with a Right-Angled Triangle at the Base Volume of a prism with an isosceles triangle at the base Rectangular Prism Right prism Regular quadrangular prism Cylinder Cylinder with inscribed prism problems

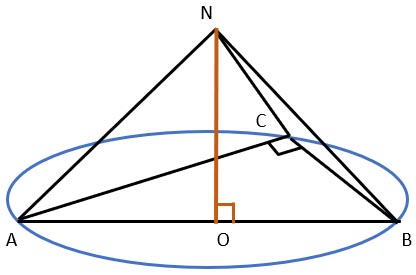
Task The base of the pyramid is a right triangle, one of the legs of which is 8 cm, and the radius of the circle circumscribed about it is 5 cm. The base of the height of this pyramid is the midpoint of the hypotenuse. The height of the pyramid is 12 cm. Calculate the lateral edges of the pyramid.  Solution. The base of the pyramid is a right triangle. The center of the circle circumscribed about the right triangle lies on its hypotenuse. Accordingly, AB = 10 cm, AO = 5 cm. Since the height ON = 12 cm, the size of the edges AN and NB is AN2 = AO2 + ON2 AN2 = 52 + 122 AN = √169 AN = 13 Since in a right triangle the hypotenuse is simultaneously the diameter of the circumscribed circle, and OC will also be the radius of the circumscribed circle, then Since we know the value AO = OB = 5 cm and the value of one of the legs of the base (8 cm), the height dropped onto the hypotenuse will equal AB = 2R = 10 R = 5 CO = 5 cm Accordingly, the value of the edge CN will be equal to CN2 =  CO2 + NO2 CN2 = 25 + 144 CN = √169 Answer: 13, 13 , 13 Task The base of the pyramid is a right triangle, the legs of which are 8 and 6 cm. The height of the pyramid is 10 cm. Calculate the volume of the pyramid. Solution. The volume of the pyramid is found by the formula: V = 1/3 Sh The area of ​​the base is found by the formula for finding the area of ​​a right triangle: S = ab/2 = 8 * 6 / 2 = 24 whence V = 1/3 * 24 *10 = 80 cm3 . 0    Regular tetrahedron | Описание курса | Prism. Parallelepiped. Cube. Solving problems

Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!