Volume of a Regular Triangular Prism (with a Regular Triangle at the Base)

To find the volume of a regular triangular prism, you can use various formulas that involve the sides of the base, the radius of the inscribed
and circumscribed circles, and the height of the prism.

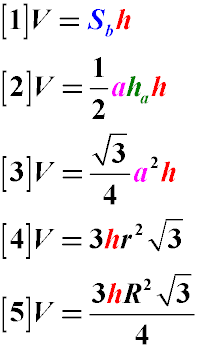
where:

• V is the volume of the regular triangular prism,
• a is the side length of the base,
• h_a is the height of the base, lowered to the side of the base,
• h is the height of the prism
• r is the radius of the circle inscribed in the base
• R is the radius of the circle circumscribed around the base of the regular triangular prism

Formulas for Finding the Volume of a Regular Triangular Prism

1. Volume through the Height of the Base: The volume of a regular triangular prism can be calculated as the product of half the side
   of the base by the height lowered from the vertex of the base to one of its sides, and multiplied by the height of the prism (Formula 2)
2. Volume through the Side Length: The volume of a regular triangular prism can be calculated as the product of the square root
   of three divided by 4, multiplied by the square of the side of the base, and multiplied by the height of the prism (Formula 3)
3. Volume through the Radius of the Inscribed Circle: The volume of a regular triangular prism can be calculated as three times
   the square root of three, multiplied by the square of the radius of the circle inscribed in the base, and multiplied by the height of
   the prism (Formula 4)
4. Volume through the Radius of the Circumscribed Circle: The volume of a regular triangular prism can be calculated as three times
   the square root of three, multiplied by the square of the radius of the circle circumscribed around the base, multiplied by the height of
   the prism, and divided by 4 (Formula 5)

Additional Explanations

• Regular Triangular Prism: A regular triangular prism is a prism with a regular triangle (equilateral triangle) as its base. This means all
  sides of the base triangle are equal, and all angles are 60 degrees.

• Height of the Base: The height of the base (h_a) is the perpendicular distance from one vertex of the triangle to the opposite side (altitude).

• Inscribed and Circumscribed Circles: The inscribed circle is the largest circle that fits inside the triangle, touching all three sides.
  The circumscribed circle is the circle that passes through all three vertices of the triangle.

These formulas provide a comprehensive approach to calculating the volume of a regular triangular prism using different geometric properties.