Cosine of a Double Angle

In the process of solving problems involving the transformation of trigonometric functions, it is sometimes necessary
to express the value of a double angle in terms of a single angle. For example, the cosine of 2α2\alpha must
be transformed into an expression where the argument of the trigonometric function is α\alpha (a single angle).

Below are the trigonometric transformations of the cosine of a double angle.

Formulas for Cosine of a Double Angle

The following are the formulas (identities) for transforming the cosine of a double angle into an expression with a single
value of this angle:

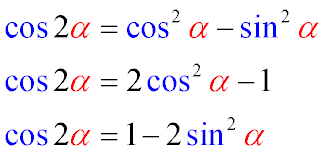
Why is this Needed?

These transformations (identities) often help to obtain the exact value for angles that cannot always be found in the table
of values of trigonometric functions.

For example, let's calculate the value of the cosine of 120 degrees.

To do this, we take the value of the cosine of 60 degrees, which is known.

If we express cos⁡(120°) as the cosine of a double angle:

We can obtain the exact value for this angle by applying the formulas mentioned above.

Using the formula cos⁡( 2α )=2 cos⁡²( α )−1:

cos⁡( 120° )=cos⁡( 2×60°) = 2 cos⁡²( 60° )−1

Since the value of cos⁡( 60° ) = 1 / 2, we calculate the resulting expression:

2 cos² 60º - 1 = 2 ( 1/2 )²  - 1 = 2 х 1/4 - 1 = -1/2

Thus,

By analogy, using the formulas for the cosine of a double angle, we can solve trigonometric equations
and find the values of double angles of trigonometric functions based on the values already known to us.