Список предметов
Height of a Triangle
18 / 67
Note. This lesson contains a description of the properties and formulas for finding the height of a triangle, as well as examples of solving problems.
If you have not found a solution to the corresponding problem, please write about it on the forum. The course will probably be supplemented.

Height of a Triangle

The height of a triangle is a perpendicular dropped from the vertex of a triangle to the opposite side or to its extension.

Properties of the Height of a Triangle

  1. If two heights in a triangle are equal, then such a triangle is isosceles.
  2. In any triangle, the segment connecting the bases of two heights cuts off a triangle similar to the original one.
  3. In a triangle, a segment connecting the bases of two altitudes that lie on two sides that are not parallel to the third side, with which it
    has no common points, can always be drawn through its two ends and the two vertices of this side.
  4. In an acute triangle, two of its altitudes cut off similar triangles from it.
  5. The minimum altitude in a triangle always passes inside this triangle.
The height of a triangle is a perpendicular dropped from the vertex of a triangle and drawn to the side opposite the vertex or to its extension.

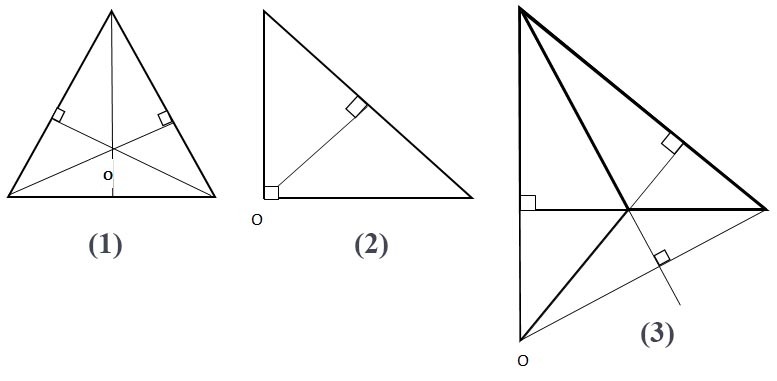
Orthocenter of a Triangle

All three altitudes of a triangle (drawn from three vertices) intersect at one point, which is called the orthocenter. To find the point of intersection
of the altitudes, it is enough to draw two altitudes (two straight lines intersect at only one point).

The location of the orthocenter is determined by the type of triangle:

  • In an acute triangle, the point of intersection of the altitudes is in the plane of the triangle (Fig. 1).
  • In a right-angled triangle, the point of intersection of the altitudes coincides with the vertex of the right angle (Fig. 2).
  • In an obtuse triangle, the point of intersection of the altitudes is located outside the plane of the triangle (Fig. 3).
  • In an isosceles triangle, the median, bisector, and altitude drawn to the base of the triangle coincide.
  • In an equilateral triangle, all three important lines (altitude, bisector, and median) coincide, and the three important points (the orthocenter,
    center of gravity, and center of the inscribed and circumcircles) are at the same intersection point of the important lines, i.e., they also coincide.

Formulas for finding the height of a triangle

Arbitrary triangle ABC with the height drawn to side a and the designations of sides and angles

The figure is given to facilitate the perception of formulas for finding the height of a triangle.
Произвольный треугольник ABC с проведенной высотой к стороне a и обозначениями сторон и углов
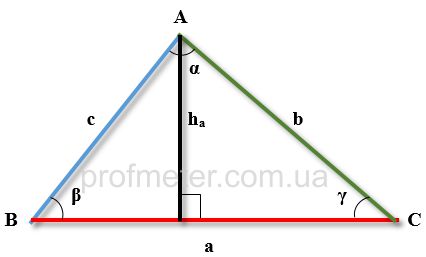
The height in the formulas is denoted by the letter h, the subscript of which corresponds to the side from which it is omitted.

Other designations:
a,b,c - lengths of the sides of the triangle
ha - height of the triangle drawn to side a from the opposite corner
hb - height drawn to side b
hc - height drawn to side c
R - radius of the circumscribed circle
r - radius of the inscribed circle

Формулы нахождения высоты произвольного треугольника, соотношений высот и длин сторон, нахождения высоты через площадь треугольника

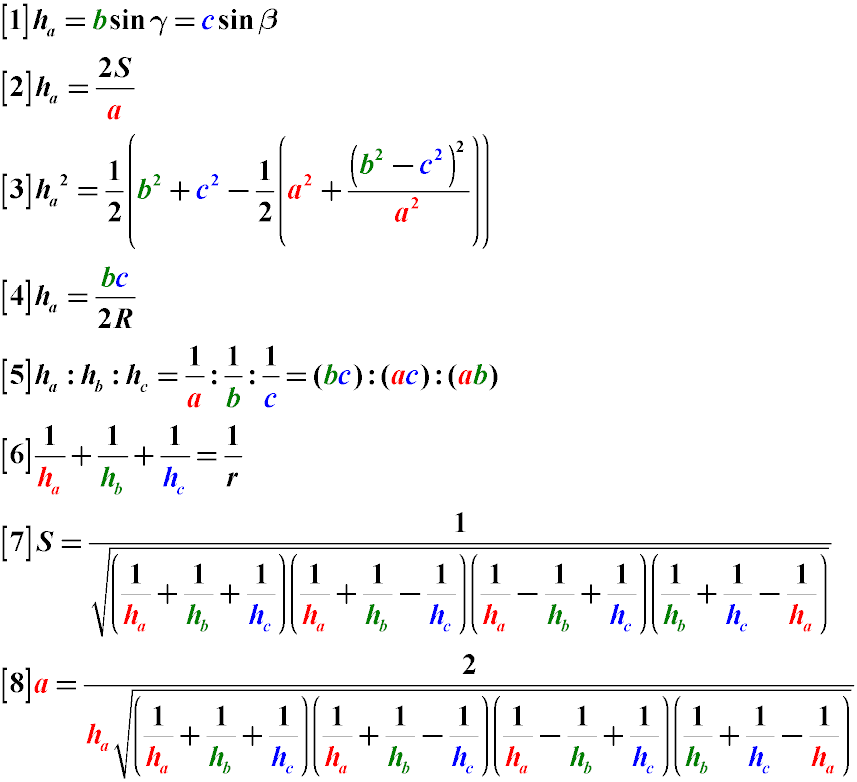
Explanations to the formulas.

The height of a triangle is equal to the product of the length of the side adjacent to the angle from which this height is lowered by the sine
of the angle between this side and the side to which this height is lowered (Formula 1)
The height of a triangle is equal to the quotient of dividing twice the area of ​​the triangle by the length of the side to which this height is
lowered (Formula 2)
The height of a triangle is equal to the quotient of dividing the product of the sides adjacent to the angle from which this height is subtracted
by twice the radius of the circle described around it (Formula 4).
The heights of the sides in a triangle are related to each other in the same proportion as the inverse proportions of the lengths of the sides
of the same triangle are related to each other, and the products of pairs of triangle sides that have a common angle are related to each
other in the same proportion (Formula 5).
The sum of the inverse values ​​of the heights of a triangle is equal to the inverse value of the radius of the circle inscribed in such a triangle
(Formula 6)
The area of ​​a triangle can be found through the lengths of the heights of this triangle (Formula 7)
The length of the side of the triangle, on which the height is lowered, can be found by applying formulas 7 and 2.

Tasks related to the similarity of triangles

In a right triangle ABC (angle C = 90 degrees), the altitude CD is drawn. Determine CD if AD = 9 cm, BD = 16 cm

Solution.

Determine the length of AB: Since AD ​​and BD are parts of the hypotenuse AB, we can find AB by adding AD and BD:
AB=AD+BD=9 cm+16 cm=25 cm

Use the Pythagorean Theorem: In a right triangle ABC, where angle C = 90°, we can use the Pythagorean Theorem
to find the lengths of legs AC and BC. But first we need to find the length of CD.

Use the properties of similarity of triangles: Triangles ADC and BDC are similar to triangle ABC because
they have one common angle (angle C) and both have a right angle (angle D).

So, we can write the ratio of the sides:
CD / AD = BC / AB
CD / BD = BC / AB
that is:

DC2=AD*BD

DC2=9*16

DC=12 cm

Problem of application of Pythagoras' theorem

Triangle ABC is right-angled. In this C-right angle. From it the altitude CD = 6cm is drawn. The difference of segments BD-AD=5 cm.

Find: Sides of triangle ABC.

Прямокутний трикутник із висотою, опущеною на гіпотенузу


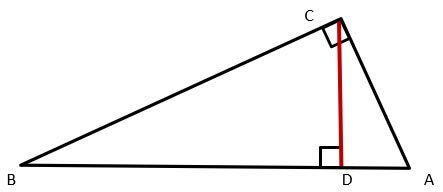
Solution

  • Let's compose a system of equations according to the Pythagorean theorem

 CD2+BD2=BC2
CD2+AD2=AC2

we have five unknowns, but since CD=6

36+BD2=BC2
36+AD2=AC2

we have four unknowns, but,
since BD-AD=5, then

BD = AD+5, then the system of equations looks like this:

36+(AD+5)2=BC2
36+AD2=AC2

we have three unknowns.

36+(AD+5)2=BC2
36+AD2=AC2

Let's compose the first and second equations.
(if you are not familiar with this technique, know that in a system of equations, these equations can be added together
and proceed to solving one equation)

Since the left part is added to the left, and the right part to the right, the equality will not be violated.
We get:

36+36+(AD+5)2+AD2=AC2+BC2

72+(AD+5)2+AD2=AC2+BC2

  • Let's write an equation for triangle ABC

Looking at the original drawing of triangle ABC, according to the Pythagorean theorem,
the following equality must hold:

AC2+BC2=AB2

Since AB=BD+AD, the equation will look like this:

AC2+BC2=(AD+BD)2

Since BD-AD=5, then BD = AD+5, then

AC2+BC2=(AD+AD+5)2 

  • Now let's look at the results we obtained when solving the first and second parts of the solution.

Namely:

72+(AD+5)2+AD2=AC2+BC2
AC2+BC2=(AD+AD+5)2

They have a common part AC2+BC2 . ТIn a way, we equate them to each other.

72+(AD+5)2+AD2= (AD+AD+5)2

72+AD2+10AD+25+AD2=4AD2+20AD+25

-2AD2-10AD+72=0 

In the resulting quadratic equation, the discriminant is D=676, respectively, the roots of the equation are:

х1=-3,5

x2=4 

Since the length of the segment can be negative, we discard the first root.

AD=4

  • Let's find the lengths of the segments:

AD=4 cm,
BD=4+5=9 cm

  • Let's find the length of the hypotenuse AB:

AB=AD+BD=4 cm+9 cm=13 cm

  • Let's find the lengths of the legs AC and BC: Use the Pythagorean theorem for a triangle △ABC

Using the Pythagorean theorem, we find the remaining sides of the triangle:

CD2+BD2=BC2

62+92=BC2

36+81=BC2

BC = √(117).


CD2+AD2=AC2

62+42 = AC2

36+16=AC2

AC = √(52)

0  


 Finding area using medians | Описание курса | Area of ​​a triangle