|
|
Regular Quadrangular Prism
Definition:
A regular quadrangular prism is a three-dimensional geometric figure with two parallel, congruent square bases and four lateral faces that are rectangles.
This type of prism is also known as a right square prism.
Key Features:
-
Lateral Edge: The lateral edge is the common side shared by two adjacent lateral faces. In a regular quadrangular prism, all lateral edges are
of equal length and perpendicular to the bases.
-
Height: The height of the prism is the perpendicular distance between the two bases. It is the length of the segment that connects corresponding
points on the two bases and is perpendicular to both.
-
Diagonal of the Prism: A diagonal of the prism is a line segment that connects two vertices of the bases that do not lie on the same face.
This diagonal spans across the interior of the prism.
-
Diagonal Plane: A diagonal plane is a plane that passes through a diagonal of the prism and includes the lateral edges. This plane divides
the prism into two symmetrical parts.
-
Diagonal Section: The diagonal section is the intersection of the prism with a diagonal plane. In a regular quadrangular prism, this section forms
a rectangle.
-
Perpendicular Section (Orthogonal Section): A perpendicular section is the intersection of the prism with a plane that is perpendicular to its lateral edges.
This section is typically a square, as it cuts through the prism parallel to the bases.
Additional Information:
-
Surface Area: The total surface area of a regular quadrangular prism is the sum of the areas of its two bases and its four lateral faces. The formula
for the surface area (A) is:
A=2a2+4ah
where (a) is the side length of the square base and (h) is the height of the prism.
-
Volume: The volume (V) of the prism is given by the product of the area of the base and the height:
V=a2h
-
Properties: All angles between the lateral faces and the bases are right angles. The prism is symmetrical along any plane that passes through its height
and divides it into two equal halves.
Elements of a regular quadrangular prism
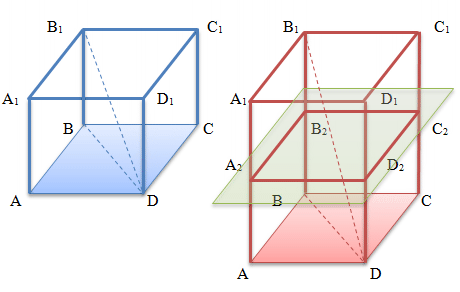
The figure shows two regular quadrangular prisms, which are designated by the corresponding letters:
- Base ABCD and A1B1C1D1 are equal and parallel to each other
-
Lateral faces AA1D1D, AA1B1B, BB1C1C and CC1D1D, each of which is a rectangle
-
Lateral surface is the sum of the areas of all lateral faces of the prism
-
Total surface is the sum of the areas of all bases and lateral faces (the sum of the area of the lateral surface and bases)
-
Lateral edges AA1, BB1, CC1 and DD1.
-
Diagonal B1D
-
Base diagonal BD
-
Diagonal section BB1D1D
-
Perpendicular section A2B2C2D2 .
Properties of a Regular Quadrangular Prism
-
Bases:
- The bases are two equal squares.
- The bases are parallel to each other.
-
Lateral Faces:
- The lateral faces are rectangles.
- The lateral faces are equal to each other.
- The lateral faces are perpendicular to the bases.
-
Lateral Edges:
- The lateral edges are parallel to each other and equal in length.
-
Perpendicular Section:
- The perpendicular section is perpendicular to all lateral edges and parallel to the bases.
- The angles of the perpendicular section are right angles.
-
Diagonal Section:
- The diagonal section of a regular quadrangular prism is a rectangle.
-
Orthogonal Section:
- The perpendicular (orthogonal) section is parallel to the bases.
-
Additional Properties:
- The prism has 6 faces, 12 edges, and 8 vertices.
- The volume of the prism is calculated as the product of the base area and the height:
V=Ab⋅h
, where (Ab) is the area of the base and (h) is the height.
- The total surface area is the sum of the lateral surface area and twice the base area:
S=2Ab+Al
, where (Al) is the lateral surface area.
Formulas for a regular quadrangular prism
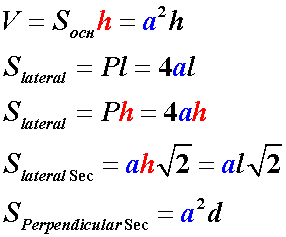
Instructions for solving problems
When solving problems on the topic "regular quadrangular prism" it is implied that:
A regular prism is a prism with a regular polygon as its base, and the lateral edges are perpendicular to the planes of the base. That is, a regular quadrangular
prism contains a square as its base. (see properties of a regular quadrangular prism above)
Note. This is part of a lesson with problems in geometry (section stereometry - prism). The problems that cause difficulties in solving are posted here. If you need
to solve a problem in geometry that is not here, write about it in the forum. The symbol √ is used to denote the action of extracting a square root in problem solutions.
Problem.
In a regular quadrangular prism, the base area is 144 cm2, and the height is 14 cm. Find the diagonal of the prism and the total surface area.
Solution.
First, we need to find the side length of the square base.
Since the base area is a square: √144 = 12 cm.
The diagonal of the square base can be found using the Pythagorean theorem:
√( 122 + 122 ) = √288 = 12√2
Now, to find the diagonal ( D ) of the prism, which extends from one vertex of the base to the opposite vertex on the top face,
we use the Pythagorean theorem in three dimensions::
√( ( 12√2 )2 + 142 ) = 22 см
The total surface area Atotal of the prism includes the areas of the two bases and the lateral surface area.
The lateral surface area is the perimeter of the base times the height.
The perimeter Pbase of the square base is:
Pbase = 4a
Pbase = 4 times 12
Pbase = 48 cm
The lateral surface area Atotal is:
Atotal =Pbase x h
Atotal = 48x 14
Atotal = 672 cm2
The total surface area is:
Atotal = 2Abase + Alateral
Atotal = 2 x 144 + 672
Atotal = 288 + 672
Atotal = 960 cm2
Summary:
Diagonal of the prism: 22 cm,
Total surface area:960 cm2
Problem
Determine the total surface area of a regular quadrangular prism if its diagonal is 5 cm and the diagonal of the lateral face is 4 cm.
Solution
Let’s denote:
- Side length of the base ( a )
- Height of the prism ( h )
The diagonal of the base can be found using the Pythagorean theorem in the base square:
a2 + a2 = 52
2a2 = 25
a = √12,5
The diagonal of the lateral face (which is a rectangle) can be expressed as:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
The total surface area will be equal to the sum of the lateral surface area and twice the area of the base.
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Answer: 25 + 10√7 ≈ 51,46 cm2 .
Right prism |
Описание курса
| Cylinder
|

