Cosine of an Angle

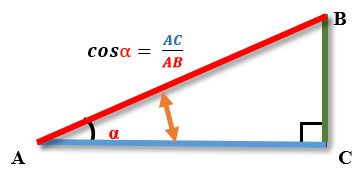
The cosine of an angle (cos) is the ratio of the adjacent leg of a right triangle to the hypotenuse.

Definition and Notation

The cosine of an angle α is denoted as cos α.
It is defined as:

Unit Circle and Cosine Function

To understand the changes in the cosine function of an angle α by quadrants, consider the movement of the movable radius OB along a circle from 0° to 360°.

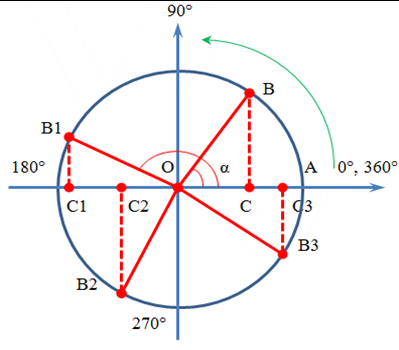
By definition:

For a unit circle, where OB = 1, this is the length of the segment OC.
Therefore, the cosine of an angle is the magnitude of the projection of the movable segment OB onto the x-axis.

The magnitude of the segment OC changes on the x-axis depending on the position of the movable radius (the magnitude of the angle).

Values of the Cosine Function by Quadrants

Let's consider the changes in the cosine function as the movable radius moves along the circle and the angle increases.
The limits of change of the cosine of the angle will be determined by quadrants.

First Quadrant (0° to 90°):

• At α = 0°, cos α = 1
• At 0° < α < 90°, 1 > cos α > 0
• At α = 90°, cos α = 0

Second Quadrant (90° to 180°):

• At α = 90°, cos α = 0
• At 90° < α < 180°, 0 > cos α > -1
• At α = 180°, cos α = -1

During the first semicircle passed by the moving radius (MR), the cosine value changes from 1 to -1.
Its largest and smallest values coincide with the length of the radius on the positive and negative semi-axes x.

Third Quadrant (180° to 270°):

• At α = 180°, cos α = -1
• At 180° < α < 270°, -1 < cos α < 0
• At α = 270°, cos α = 0

Fourth Quadrant (270° to 360°):

• At α = 270°, cos α = 0
• At 270° < α < 360°, 0 < cos α < 1
• At α = 360°, cos α = 1

During the second semicircle, the cosine value changes from -1 to 1.
Its smallest and largest values coincide with the length of the radius on the negative and positive semi-axes x.

Complete Revolution

During the entire revolution of the moving radius OB, from the coincidence with OA to their second coincidence, the angle numerically changes from 0° to 360°,
and the numerical value of the cosine of the angle changes within the limit from 1 to -1.

Properties of Sine and Cosine Functions

The numerical value of the sine and cosine of an angle depends only on the degree measure of the angle and does not depend on the parameters
of the right triangle and its location on the plane. The sine and cosine functions of an angle do not exceed 1 in numerical value.

It is always possible to calculate the values of the sine and cosine of any acute angle of a right triangle if the lengths of its legs and hypotenuse are known.
However, more often, calculations are not performed manually; instead, the values of the functions are read from tables of logarithms of trigonometric
functions depending on the size of the acute angle.

Values ​​of the cosine of angle α