|
|
Right Triangle
A right triangle is a triangle in which one of the angles is a right angle, i.e., equal to 90 degrees.
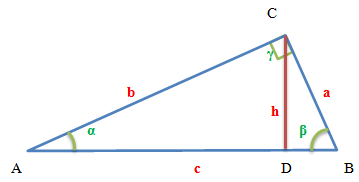
Elements of a Right Triangle
- Hypotenuse: The side opposite the right angle is called the hypotenuse (denoted as cc or AB in the figure).
- Legs: The sides adjacent to the right angle are called the legs. Each right triangle has two legs (denoted as a and b
or AC and BC in the figure).
Formulas and Properties of a Right Triangle
Formulas for a right triangle - altitude, radius of the inscribed and circumscribed circle, trigonometric relationships.
Formula designations:
 (see the figure above) (see the figure above)
a, b - legs of a right triangle
c - hypotenuse
α, β - acute angles of a triangle
S - area
h - height dropped from the vertex of a right angle to the hypotenuse
ma - median drawn to side a from the opposite angle (α)
mb - median drawn to side b from the opposite angle (β)
mc - median drawn to side c from the opposite angle (γ)
In a right triangle, any of the legs is less than the hypotenuse (Formulas 1 and 2).
This property is a consequence of the Pythagorean theorem.
The cosine of any of the acute angles is less than one (Formulas 3 and 4).
This property follows from the previous one. Since any of the legs is less than
the hypotenuse, the ratio of the leg to the hypotenuse is always less than one.
The square of the hypotenuse is equal to the sum of the squares of the legs
(Pythagorean theorem). (Formula 5).
This property is constantly used when solving problems.
The area of a right triangle is equal to half the product of the legs (Formula 6)
The sum of the squares of the medians to the legs is equal to five squares of
the median to the hypotenuse and five squares of the hypotenuse, divided by
four (Formula 7). In addition to the specified one, there are 5 more formulas, so
it is recommended that you also familiarize yourself with the lesson "Median of
a Right Triangle", which describes the properties of the median in more detail.
The height of a right triangle is equal to the product of the legs, divided by
the hypotenuse (Formula 8)
The squares of the legs are inversely proportional to the square of the height
dropped to the hypotenuse (Formula 9). This identity is also one of the
consequences of the Pythagorean theorem.
The length of the hypotenuse is equal to the diameter (two radii) of
the circumscribed circle (Formula 10). The hypotenuse of a right triangle is
the diameter of the circumscribed circle. This property is often used to
solve problems.
The radius of a circle inscribed in a right triangle can be found as half of
the expression that includes the sum of the legs of this triangle minus the
length of the hypotenuse. Or as the product of the legs divided by the sum of
all sides (the perimeter) of this triangle. (Formula 11)
The sine of angle A (α, alpha) in a right triangle will be equal to the ratio of
the leg opposite this angle to the hypotenuse (by definition of sine). (Formula 12).
This property is used to solve problems. Knowing the lengths of the sides, you
can find the angle they form.
The cosine of angle A (α, alpha) in a right triangle will be equal to the ratio of
the leg adjacent to this angle to the hypotenuse (by definition of sine). (Formula 13)
See also The relationship between the angles and sides of a right triangle is
studied by Trigonometry.
Problems on finding the area of an arbitrary triangle |
Описание курса
| Hypotenuse of a right triangle
|

