|
|
Triangle
Triangle and Its Properties
Variations for Defining the Concept of "Triangle"
Basic Definition: A triangle is a figure consisting of three points that do not lie on the same line, connected in pairs
by line segments. The points are called the vertices of the triangle, and the segments are called the sides of the triangle.
Geometric Definition: A triangle is a figure formed by line segments connecting three points that do not lie on the same line.
Planar Definition: A triangle is a part of the plane bounded by three line segments.
Detailed Explanation
A triangle is one of the most fundamental shapes in geometry. It is a polygon with three edges and three vertices.
The basic properties and types of triangles are essential in various fields such as mathematics, engineering, architecture,
and art.
Properties of a Triangle
- Vertices and Sides:
- Vertices: The three points where the sides of a triangle meet are called vertices. They are usually denoted by
capital letters (e.g., A, B, C).
- Sides: The line segments connecting the vertices are called sides. They are usually denoted by lowercase
letters corresponding to the opposite vertices (e.g., a, b, c).
-
Angles:
-
A triangle has three interior angles. The sum of the interior angles of a triangle is always 180 degrees.
-
The angles are usually denoted by Greek letters (e.g., α, β, γ).
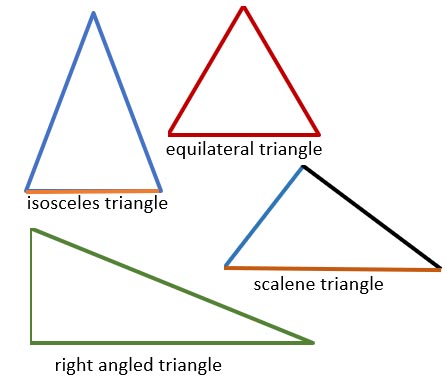
- Types of Triangles by Sides:
- Equilateral Triangle: All three sides are equal, and all three interior angles are 60 degrees.
- Isosceles Triangle: Two sides are equal, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides are of different lengths, and all three interior angles are different.
- Types of Triangles by Angles:
- Acute Triangle: All three interior angles are less than 90 degrees.
- Right Triangle: One of the interior angles is exactly 90 degrees.
- Obtuse Triangle: One of the interior angles is greater than 90 degrees.
- Perimeter and Area:
Perimeter: The perimeter of a triangle is the sum of the lengths of its sides
Notation and Naming Conventions
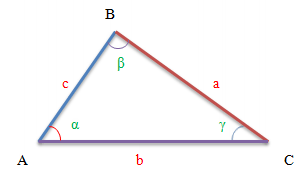
In geometry problems, a triangle with vertices A, B, and C is denoted as triangle ABC. Each of the sides is denoted by the name
of the points that it connects. Accordingly, triangle ABC has sides:
The angles of a triangle can be denoted by the names of the points that form the given angle, or by the name of the point that
is the vertex of the angle. The angles can also be assigned the names of letters of the Greek alphabet. For example:
-
∠A is the same as ∠BAC and the same as α
-
∠B is the same as ∠ABC and the same as β
-
∠C is the same as ∠BCA and the same as γ
Side and Angle Notations in Formulas
In geometric formulas, notations are used that sometimes confuse students. The letter a denotes the side opposite angle A,
the letter b denotes the side opposite angle B, and the letter c denotes the side opposite angle C. This notation helps in
applying various trigonometric and geometric formulas accurately.
Special Points in a Triangle
- Centroid: The point where the three medians of the triangle intersect. It is the center of mass of the triangle.
- Circumcenter: The point where the perpendicular bisectors of the sides intersect. It is the center of the circle that
passes through all three vertices of the triangle.
- Incenter: The point where the angle bisectors of the triangle intersect. It is the center of the circle that is tangent to
all three sides of the triangle.
- Orthocenter: The point where the altitudes of the triangle intersect.
Understanding these properties and notations is crucial for solving various geometry problems involving triangles. If you
have any specific questions or need further explanations, feel free to ask on the forum!
Ellipse |
Описание курса
| Median of a triangle
|

