|
|
Right-Angled Trapezoid
Basic Concepts, Properties, and Formulas
A right-angled trapezoid is a trapezoid in which at least one of the angles is a right angle (classical definition).
Note: In fact, a right-angled trapezoid has at least two right angles (see properties below).
Other definitions:
-
A trapezoid is called right-angled if one of its lateral sides is perpendicular to the bases.
-
A trapezoid that has right angles at the lateral side is called right-angled.
Formulas for Right-Angled Trapezoid
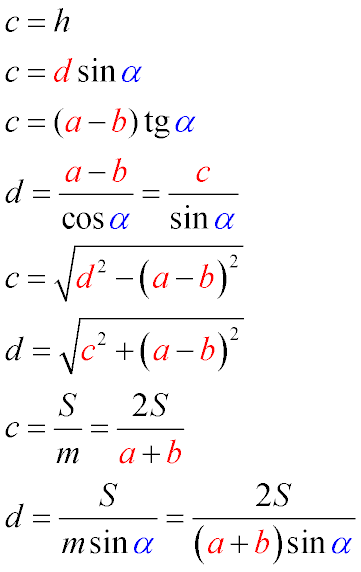
Formulas for finding the height and lateral side of a right-angled trapezoid through the bases and the acute angle. The notation of the formulas is given in the drawing above. Accordingly:
- a and b – bases of the trapezoid
- c – lateral side of the right-angled trapezoid, perpendicular to the bases
- d – lateral side of the trapezoid that is not perpendicular to the bases
- α – acute angle at the larger base of the trapezoid
- m – median line of the trapezoid
Interpretation of the formulas:
-
The lateral side of the right-angled trapezoid, perpendicular to the bases, is equal to the height of the trapezoid (Formula 1).
-
The lateral side of the right-angled trapezoid, perpendicular to the bases, is equal to the product of the sine of the acute angle at the larger base and the length of the other lateral side. (Triangle CKD is right-angled, hence h/d=sin α according to the properties of the sine, and c = h) (Formula 2).
-
The lateral side, perpendicular to the bases, is equal to the product of the difference of the bases and the tangent of the acute angle at the larger base. (Triangle CKD is right-angled. Since the trapezoid is right-angled, the length KD is the difference of the bases, and h/KD=tan α by the definition of the tangent, and c = h, hence c/KD=tan α) (Formula 3).
-
The lateral side that is not perpendicular to the bases is equal to the quotient of the difference of the bases by the cosine of the acute angle at the larger base or the quotient of the height of the trapezoid and the sine of the acute angle at the larger base. (The difference of the bases is KD. In the right-angled triangle CKD, by the definition of the cosine, cos α=KD/d, hence the desired formula) (Formula 4).
-
The lateral side of the right-angled trapezoid that is not perpendicular to the bases is equal to the square root of the difference of the square of the other lateral side and the square of the difference of the bases. (The difference of the bases is KD, KC is the other lateral side. Triangle CKD, further – a consequence of the Pythagorean theorem – from the square of the hypotenuse we subtract the square of the leg and extract the square root from the resulting expression, we find the desired leg) (Formula 5).
-
The lateral side of the right-angled trapezoid, perpendicular to the bases, is equal to the square root of the sum of the square of the other lateral side and the square of the difference of the bases. (The difference of the bases is KD, KC is the other lateral side. Triangle CKD, right-angled, further – a consequence of the Pythagorean theorem – we find the sum of the squares of the legs and extract the square root from the resulting expression) (Formula 6).
-
The lateral side of the right-angled trapezoid, perpendicular to the bases, is equal to the quotient of the double area of the trapezoid by the sum of its bases. (Since the area of the trapezoid is equal to the product of the median line of the trapezoid and the height (S = mh), and h = c, then dividing the area by the median line of the right-angled trapezoid, we get its height, and substituting the value of the median line into the formula (m = (a + b) / 2), we get the desired formula) (Formula 7).
-
The lateral side of the right-angled trapezoid that is not perpendicular to the bases is equal to the quotient of the double area of the trapezoid by the product of the sum of its bases and the sine of the acute angle at the base. (Since the area of the trapezoid is equal to the product of the median line of the trapezoid and the height (S = mh), and h = c, then dividing the area by the median line of the right-angled trapezoid, we get its height, and expressing the height through the other lateral side and substituting the value of the median line into the formula (m = (a + b) / 2), we get the desired formula) (Formula 8).
Since a right-angled trapezoid is a special case of a trapezoid, other formulas and properties can be found in the section "Trapezoid".
Properties of Right-Angled Trapezoid
-
A right-angled trapezoid has two right angles.
-
Both right angles of a right-angled trapezoid necessarily belong to adjacent vertices.
-
Both right angles in a right-angled trapezoid necessarily adjoin the same lateral side.
-
The diagonals of a right-angled trapezoid form a right triangle with one of the lateral sides.
-
The length of the lateral side of the trapezoid, perpendicular to the bases, is equal to its height.
-
In a right-angled trapezoid, the bases are parallel, one lateral side is perpendicular to the bases, and the other lateral side is inclined to the bases.
-
A right-angled trapezoid has two right angles, and the other two angles are acute and obtuse.
Problem
In a right-angled trapezoid, the larger lateral side is equal to the sum of the bases, and the height is 12 cm. Find the area of the rectangle whose sides
are equal to the bases of the trapezoid.
Solution:
Let us denote the trapezoid as ABCD. Let us denote the lengths of the bases of the trapezoid as a (larger base AD) and b (smaller base BC).
Let the right angle be ∠A.
The area of the rectangle whose sides are equal to the bases of the trapezoid will be:
S = ab
From the vertex C of the upper base of the trapezoid ABCD, we drop the height CK to the lower base. The height of the trapezoid is known from
the condition of the problem. Then, by the Pythagorean theorem:
CK2+KD2=CD2
Since the larger lateral side of the trapezoid is equal to the sum of the bases, CD = a + b.
Since the trapezoid is right-angled, the height drawn from the upper base of the trapezoid divides the lower base into two segments AD = AK + KD.
The length of the first segment is equal to the smaller base of the trapezoid, as the height formed the rectangle ABCK, i.e., BC = AK = b,
hence, KD will be equal to the difference in the lengths of the bases of the right-angled trapezoid KD = a - b.
Thus,
122+(a−b)2=(a+b)2
from which
144+a2−2ab+b2=a2+2ab+b2
144 = 4ab
Since the area of the rectangle S = ab (see above), then
144 = 4S
S=144/4=36S = 144 / 4 = 36
Answer: 36 cm².
Diagonals of a trapezoid |
Описание курса
| Polygons
|

