AXIOM 8

THE EXISTENCE OF A TRIANGLE EQUAL TO A GIVEN

Whatever the triangle is, there exists a triangle equal to it at a given location relative to a given ray.

Given any direction of a line, a triangle equal to the given one can always be constructed on it.

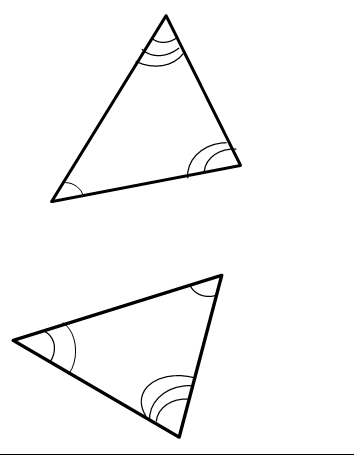
Two triangles may differ from each other in the lengths of their sides and the degrees of their angles, but their location on the plane (orientation)
does not affect the equality or inequality of the triangles.

Triangles are called equal if their corresponding sides and angles are equal.

Additional Information

1. Copying a Triangle: To construct a triangle equal to a given one, you can use the copying method. This involves measuring all the sides and angles
   of the original triangle and constructing a new triangle with the same dimensions.

2. Rotation and Reflection: Congruent triangles can be obtained by rotating or reflecting the original triangle. These operations do not change the
   lengths of the sides and angles of the triangle, so the resulting triangles remain equal to the original.

3. Practical Application: In geometry and engineering, it is often necessary to construct congruent triangles for various tasks, such as creating
   symmetrical structures or checking the correctness of constructions.

4. Triangle Congruence Theorem: There are several theorems that help determine the congruence of triangles, such as the three-side congruence
   theorem (SSS), the two-side congruence theorem (SAS), and the two-angle congruence theorem (ASA).

5. Angles and Perimeters of Congruent Triangles: Congruent triangles have equal angles opposite corresponding sides. The figure shows congruent
   triangles, but oriented differently in the plane. Congruent triangles also have equal perimeters.

6. Symmetry and Transformations: Symmetry plays a crucial role in understanding congruent triangles. Transformations such as translations, rotations,
   and reflections can be used to map one triangle onto another, demonstrating their congruence.

7. Real-World Examples: Congruent triangles are used in various real-world applications, including architectural design, engineering projects, and even
   in art. Understanding the properties of congruent triangles helps in creating accurate and aesthetically pleasing designs.