AXIOM 1

Point–line–plane postulate

Whatever the straight line, there are points belonging to this line, and points not belonging to it. There is exactly one line passing through two distinct points

This statement is an axiom, that is, it is initially accepted as true and can not be proved.

Comments

In the figure below, designated points A and B. At this point A belongs line a, and the point B - does not belong.The points are marked in blue, the straight line in red.
Note. Point in the figures are usually denoted by capital letters, and lines - in lower case.


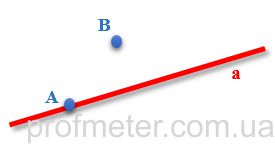
If the point belongs to a straight line (Fig.1), then the short entry is: A ∈ a (read as: "point A belongs to the straight line" a "). If the point does not belong to a straight line, then the short entry is: B ∉ a (read as: "B does not belong to the straight line a").

The points belonging or not belonging to the line in the plane

Unique line assumption

Through any two points you can draw a straight line, and only one. There is exactly one line passing through two distinct points.



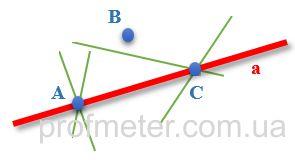
If two non-coinciding points (A and C) are taken, then only one straight line (a) can be drawn through them, although an infinite number of straight lines can be drawn through each of these points (Fig.2)

Note. When the two points belong to the line (in this case A and C), it can also be described as a straight AC, it should be understood that identification of a (lower case letter a) and AC refers to the same line.
Explanation. Since the two points (see. Axiom) can hold only one straight line, the symbols of this line may be a few, but the meaning remains the same.

Straight through a point.
If the points A and C coincide (in this case one point will be denoted by two letters), then through them one can draw an infinite number of straight lines.

The axiom described above is the basis for the Euclidean geometry. On the basis of this axiom, proofs of many theorems are constructed.