|
|
Note. This chapter contains the formulation and proof of the sine theorem. In the lessons of the chapter, we give problems on geometry with solutions on the same topic.
See also the theorem of cosines.
The sine theorem
The sine theorem establishes the relationship between the angles of the triangle and the sides opposite to it.
The formulation of the sine theorem
The sides of the triangle are proportional to the sines of the opposite angles
or,
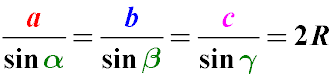
Where
R is the radius of a circumcircle circumscribed around a triangle
a, b, c - sides of the triangle
α, β, γ are the values of the angles opposite to these sides
Proof of the sine theorem
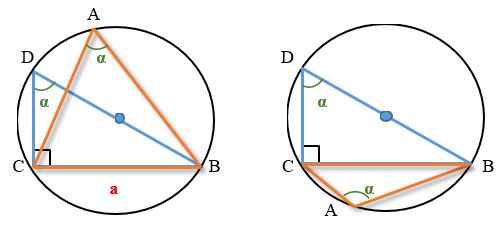
The proof of the sine theorem occurs with the aid of additional constructions.
We construct an arbitrary triangle inscribed in a circle. Denote it as ABC.
In addition, we construct the diameter of the circle into which an arbitrary triangle is inscribed, but so that it passes through one of its angles. The diameter is equal to the double radius of the circle (2R).
Let's take into account that one of the properties of a right-angled triangle inscribed in a circle is that its hypotenuse is the diameter of the circle into which it is inscribed.
Denote the diameter for the circumscribed circle as BD. The resulting triangle BCD is rectangular, since its hypotenuse lies on the diameter of the circumscribed circle (the property of the angles inscribed in the circle).
Thus, the additionally constructed triangle, in which one common side with the previously constructed arbitrary triangle, and the hypotenuse coincides with the diameter of the circle, is rectangular. That is, the triangle DBC is rectangular.
To prove the whole theorem, since the dimensions of the triangle ABC are chosen arbitrarily, it is sufficient to prove that the ratio of one arbitrary side to the opposite corner is equal to 2R.
Let this be 2R = a / sin α, that is, if we take 2R = BC / sin A.
Since the angles inscribed in a circle based on the same arc are equal, the angle CDB is either equal to the angle CAB (if the points A and D lie on one side of the line BC) or is equal to π-CAB (otherwise) .
Let us turn to the properties of trigonometric functions. Since sin (π - α) = sin α, the above variants of the construction of the triangle will still lead to the same result.
We calculate the value 2R = a / sin α, according to the drawing 2R = BC / sin A. To do this, replace sin A by the ratio of the corresponding sides of the right triangle.
2R = BC / sin A
2R = BC / ( BC / DB )
2R = DB
And, since DB was constructed as the diameter of a circle, equality is satisfied.
Repeating the same argument for the other two sides of the triangle, we get:
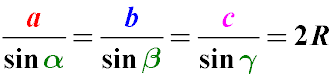
The sine theorem is proved.
Sine |
Описание курса
| Cosine
|

