|
|
Примечание. См. также таблицу значений тригонометрических функций для всех углов.
Синус 30, косинус 30, тангенс 30 градусов и синус 60, косинус 60, тангенс 60 градусов
 Как были вычислены эти значения?
Также вы можете сразу перейти к:
На этой странице приведено пошаговое пояснение логики расчета данных значений, сначала для угла тридцать градусов, а затем и шестьдесят. Для этого производится построение произвольного прямоугольного треугольника с соответствующими углами и вычисляется значение синуса, косинуса и тангенса 30 градусов, а во второй части данной статьи - для угла 60 градусов.
Значения тригонометрических функций синуса, косинуса, тангенса при α=30°
Рассмотрим равносторонний треугольник АВС. Пусть, каждая из его сторон будет равна a. Согласно свойствам равностороннего треугольника, все его углы равны, в том числе угол ∠В=60°.
Значения синуса, косинуса и тангенса мы можем вычислить, если найдем соотношение соответствующих сторон для угла 30 градусов в прямоугольном треугольнике. Так как значение этих тригонометрических функций зависит исключительно от градусной меры угла, то вычисленные нами соотношения и будут значениями синуса 30, косинуса 30 и тангенса 30 градусов.
Сначала совершим дополнительные построения. Из вершины А на сторону BC проведем медиану AO.
Медиана АО в равностороннем треугольнике одновременно является биссектрисой и высотой.
Тогда треугольник АОВ – прямоугольный с углом ∠ВАО=30°. (Угол В равен 60 градусам, ∠ВOA прямой и равен 90 градусам, следовательно, ∠ВАО = 180 - 90 - 60 = 30 градусов)
|
Значення тригонометричних функцій синуса, косинуса, тангенса при α=30°
Розглянемо рiвнобiчний трикутник АВС. Хай, кожна з його сторін буде рівна а. Згідно з властивостями рівностороннього трикутника, всі його кути рівні, у тому числі кут ∠В=60°.
Значення синуса, косинуса і тангенса ми можемо обчислити, якщо знайдемо співвідношення відповідних сторін для кута 30 градусів в прямокутному трикутнику. Оскільки значення цих тригонометричних функцій залежить виключно від градусної міри кута, то обчислені нами співвідношення і будуть значеннями синуса 30, косинуса 30 і тангенса 30 градусів.
Спочатку зробимо додаткові побудови. З вершини А на сторону BC проведемо медіану АO.
Медіана АО у рівносторонньому трикутнику одночасно є бісектрисою і висотою.
Тоді тикутник АОВ - прямокутний з кутом ∠ВАО=30°. (Кут В дорівнює 60 градусам ∠ВOA прямій і дорівнює 90 градусам, отже ∠ВАО = 180 - 90 - 60 = 30 градусів)
|
|
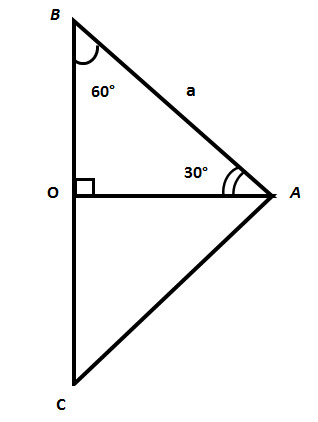
Для полученного прямоугольного треугольника вычислим значения тригонометрических функций его углов. Сделаем это сначала для угла 30 градусов.
Величина гипотенузы нам известна и равна a. Катет OB равен a/2 , так как AO - медиана треугольника ABC. Найдем катет AO.
По теореме Пифагора:
АВ2=АО2+ОВ2;
АО2=АВ2-ОВ2
подставим в полученное выражение значение гипотенузы (мы приняли, что оно равно а)
АО2=a2- (а/2)2
АО2=3a2/4
AO=√( 3a2/4 ) =a√3/2
Теперь мы вычислили все стороны прямоугольного треугольника ABO. Учитывая, что AB = a, OB = a/2, AO = a√3/2, из соотношений сторон прямоугольного треугольника рассчитаем полученные значения. Согласно определению синуса, косинуса и тангенса:
sin 30 = OB / AB (по определению синуса - отношение противолежащего катета к гипотенузе)
cos 30 = AO / AB (по определению косинуса - отношение прилежащего катета к гипотенузе)
tg 30 = OB / AO (по определению тангенса - отношение противолежащего катета к прилежащему)
Откуда:
Так как треугольник ABC - равносторонний, то BO равно AB/2, а значение AO вычислено выше. В результате получаем табличные значения sin 30, cos 30 и tg 30 градусов
|
Для отриманого прямокутного трикутника обчислимо значення тригонометричних функцій його кутів. Зробимо це спочатку для кута 30 градусів.
Величина гіпотенузи нам відома і рівна а. Катет OB рівний a/2, оскільки АO - медіана трикутника ABC. Знайдемо катет АТ.
По теоремі Піфагора:
АВ2=АО2+ОВ2;
АО2=АВ2-ОВ2
пiдставимо в одержане рiвняння значення гiпотенузи (намi прийнято, що воно равно а)
АО2=a2- (а/2)2
АО2=3a2/4
AO=√( 3a2/4 ) =a√3/2
Тепер ми обчислили всі сторони прямокутного трикутника ABO. Враховуючи, що AB = a, OB = a/2, AO = a√3/2, iз спiввiдношень сторiн прямокутного трикутника розрахуємо одержанi значення. Згiдно визначенню сiнуса, косiнуса та тангенса:
sin 30 = OB / AB (за визначенням синуса - відношення катета, що протилежить, до гіпотенузи)
cos 30 = AO / AB (за визначенням косинуса - відношення прилеглого катета до гіпотенузи)
tg 30 = OB / AO (за визначенням тангенса - відношення катета, що протилежить, до прилеглого)
Звiдки маємо:
Враховуючи, що трикутник ABC - рiвнобiчний, то BO равно AB/2, а значення AO розраховано вище. В результатi одержуємо табличнi значення sin 30, cos 30 и tg 30 градусiв
|
Табличные значения sin 30, cos 30 и tg 30 градусов:
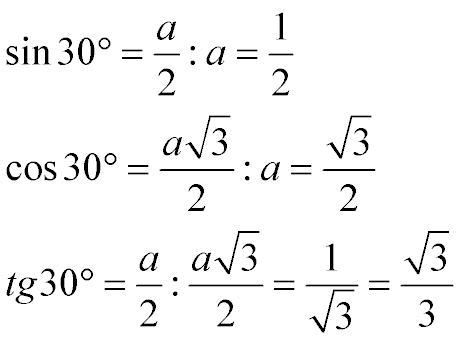
То есть:
Тангенс 30 градусов равен корню из трех на три
Синус 30 градусов равен одной второй или 0,5
Косинус 30 градусов равен корню из трех на два
Учитывая таблицу формул приведения тригонометрических функций,
Так как sin( 90°- 30°) = sin60°, а sin60°=cos30°, то:
Табличные значения sin 60, cos 60 и tg 60 градусов:
Как именно были вычислены эти функции, описано выше. Здесь же приведены сами значения:
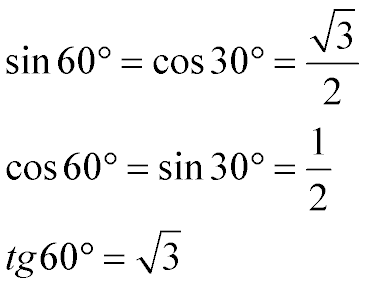
То есть:
Тангенс 60 градусов равен корню из трех
Синус 60 градусов равен корню из трех на два
Косинус 60 градусов равен одной второй или 0,5
Как видно из расчетов, приведенных выше, при вычислении значения конкретной тригонометрической функции важны не конкретные длины сторон, а только их соотношение, которое всегда будет одинаковым для одних и тех же углов, вне зависимости от размеров треугольника.
Синус, косинус и тангенс угла пи на 3 (π/3)
В задачах кроме градусной меры угла часто встречаются и обозначения угла в радианах. Радианная мера угла выражается через число пи, которое описывает соотношение длины окружности к ее диаметру. Для простоты запоминания правила перевода радиан в градусы и обратно, предлагаю всегда помнить следующее: диаметр окружности охватывает дугу величиной 180 градусов, что составляет пи радиан. Поскольку все величины угла в радианах указываются через число пи, то для перевода в градусную меру достаточно заменить число пи на 180 градусов.
Поэтому, примем во внимание, что угол пи на 3 равен 60 градусам. (180 / 3 = 60)
Откуда:
- Тангенс π/3 (пи на три) радиан равен корню из трех
- Синус π/3 (пи на три) радиан равен корню из трех на два
- Косинус π/3 (пи на три) радиан равен одной второй (1/2) или 0,5
Чтобы эти значения было удобно запомнить визуально, они приведены на рисунке ниже.
|
Тобто:
Тангенс 60 градусів дорівнює кореню з трьох
Синус 60 градусів дорівнює кореню з трьох на два
Косинус 60 градусів рівний однією другою або 0,5
Як видно з розрахунків, приведених вище, при обчисленні значення конкретної тригонометричної функції важливі не конкретні довжини сторін, а лише їх співвідношення, яке завжди буде однаковим для одних і тих же кутів, незалежно від розмірів трикутника.
Синус, косинус і тангенс кута пі на 3 (π/3)
У завданнях окрім градусної міри кута часто зустрічаються і позначення кута в радіанах. Міра радіану кута виражається через число пі, яке описує співвідношення довжини кола до її діаметру. Для простоти запам'ятовування правила переведення радіан в градуси i назад, пропоную завжди пам'ятати наступне: діаметр кола охоплює дугу величиною 180 градусів, що складає пі радіан. Оскільки всі величини кута в радіанах вказуються через число пі, то для переведення в градусну міру досить замінити число пі на 180 градусів.
Тому, візьмемо до уваги, що кут пі на 3 дорівнює 60 градусам. (180 / 3 = 60)
Звідки:
- Тангенс π/3 (пі на три) радіан дорівнює кореню з трьох
- Синус π/3 (пі на три) радіан дорівнює кореню з трьох на два
- Косинус π/3 (пі на три) радіан рівний однієї другої (1/2) або 0,5
Щоб ці значення було зручно запам'ятати візуально, вони наведені на малюнку нижче.
|

Синус, косинус и тангенс угла пи на 6 (π/6)
Исходя из написанного выше принципа перевода радиан в градусы, угол пи на 6 будет равен
180 / 6 = 30 градусов.
Откуда:
- Тангенс пи на 6 (π/6) равен корню из трех на три
- Синус пи на 6 (π/6) равен одной второй (1/2) или 0,5
- Косинус пи на 6 (π/6) равен корню из трех на два
Для более удобного визуального восприятия эти значения приведены ниже на рисунке
|
Синус, косинус і тангенс кута пі на 6 (π/6)
Виходячи з написаного вище принципу переведення радіан в градуси, кут пі на 6 дорівнюватиме
180 / 6 = 30 градусів.
Звідки:
- Тангенс пі на 6 (π/6) дорівнює кореню з трьох на три
- Синус пі на 6 (π/6) дорівнює однієї другої (1/2) або 0,5
- Косинус пі на 6 (π/6) дорівнює кореню з трьох на два
Для зручнішого візуального сприйняття ці значення приведені нижче на малюнку
|
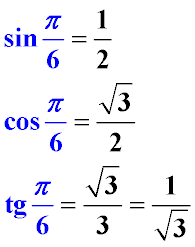
Примечание. Данная статья показывает, как вычисляется значение sin 60, cos 60 и подобных значений. Если Вы хотите посмотреть сводную справочную информацию - перейдите на таблицу значений тригонометрических функций
Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45) |
Описание курса
| Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105)
|

