|
|
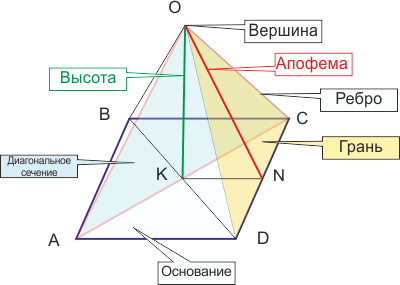
Піраміда
В даному розділі наведені формули знаходження висоти, площі, обсягу піраміди (в тому числі усіченої). Описано назви її елементів (вершина, апофема, ребро, грань, висота, діагональний перетин).
У підрозділах можна подивитися приклади розв'язання задач про піраміди.
Об'єм піраміди
Об'єм будь якой піраміди (в т.ч. трикутної) дорівнює одній третині добутку площі її основи на висоту
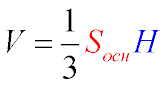
Об'єм усіченої піраміди
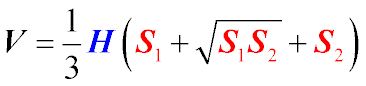
H - висота усіченої піраміди;
S1 - площа нижньої основи;
S2 - площа верхньої основи.
Властивості правильної піраміди
Піраміда називається правильною, якщо основою її є правильний багатокутник, а вершина проектується в центр основи.
Правильна піраміда має такі властивості:
- бічні ребра правильної піраміди рівні;
- в правильній піраміді всі бічні грані - рівні рівнобедрені трикутники;
- в будь-яку правильну піраміду можна вписати сферу;
- навколо будь-якої правильної піраміди можна описати сферу;
- якщо центри вписаної і описаної сфери збігаються, то сума плоских кутів при вершині піраміди дорівнює π, а кожен з них відповідно π/n, де n - кількість сторін багатокутника основи;
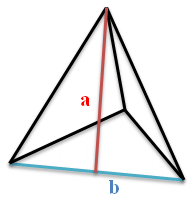
- площа бічної поверхні правильної піраміди дорівнює половині добутку периметра основи на апофему.
Як знайти площу піраміди
Площа піраміди (S) дорівнює сумі площі її основи (Sоснови) і бічній поверхні SБокПоверхнi (Формула 1)
Відповідно, так як площа бічної поверхні піраміди дорівнює сумі поверхонь всіх її граней (S1,S2...Sn), то отримуємо формулу 2.

Якщо піраміда правильна, то площі всіх її бічних граней рівні між собою. Тоді досить знайти площу основи піраміди і додати до нього площу бічної грані (SГранi), помноженої на їх кількість (n) (см. Формулу 3).
Оскільки ми знаємо, що в правильній піраміді всі грані являють собою трикутник, то, використавши формулу площі рівнобедреного трикутника, потримаємо Формулу 4 - де площа бічної поверхні піраміди буде дорівнює добутку половини периметра основи (P) на апофему (a).
Для знаходження площі правильної трикутної піраміди використовуємо формулу площі рівностороннього трикутника зі стороною b, до якої додамо площа трьох граней, що представляють собою трикутник з основою b і висотою a (вона ж апофема правильної трикутної піраміди). У підсумку отримуємо Формулу 5.
Якщо ж піраміда являє собою тетраедр, то все його грані рівні між собою і площа поверхні такої піраміди дорівнює квадрату сторони (b), помноженому на корінь з трьох (Формула 6).
Площа поверхні правильної чотирикутної піраміди знаходиться за загальним правилом - оскільки в основі лежить квадрат, то його площа дорівнює квадрату сторони основи (b), до якого додається площа чотирьох граней бічних сторін (Формула 7).
Знайшли помилку або інформація була неповною? Напишіть про це на форумі!
Призма з трикутником в основі |
Описание курса
| З трикутником в основі
|

