Примітка. Урок містить опис властивостей та формули знаходження висоти трикутника, а також приклади
розв'язання задач. Якщо Ви не знайшли вирішення відповідного завдання – пишіть про це на форумі. Напевно, курс
буде доповнено.

Висота трикутника

Висота трикутника – це перпендикуляр, опущений з вершини трикутника на протилежну сторону або її продовження.

Властивості висоти трикутника:

1. Якщо у трикутнику дві висоти рівні, то такий трикутник є рівнобедреним.
2. У будь-якому трикутнику відрізок, що з'єднує основи двох висот, відсікає трикутник, подібний до початкового.
3. У трикутнику відрізок, що з'єднує основи двох висот, які лежать на двох сторонах, непаралельних третій стороні,
   з якою він не має спільних точок, завжди можна провести коло через два його кінці та дві вершини цієї сторони.
4. У гострокутному трикутнику дві його висоти відсікають від нього подібні трикутники.
5. Мінімальна висота в трикутнику завжди проходить усередині цього трикутника.

Ортоцентр трикутника

Усі три висоти трикутника (проведені з трьох вершин) перетинаються в одній точці, яка називається ортоцентром.
Для того, щоб знайти точку перетину висот, достатньо провести дві висоти (дві прямі перетинаються лише в одній точці).

Розташування ортоцентра визначається видом трикутника:

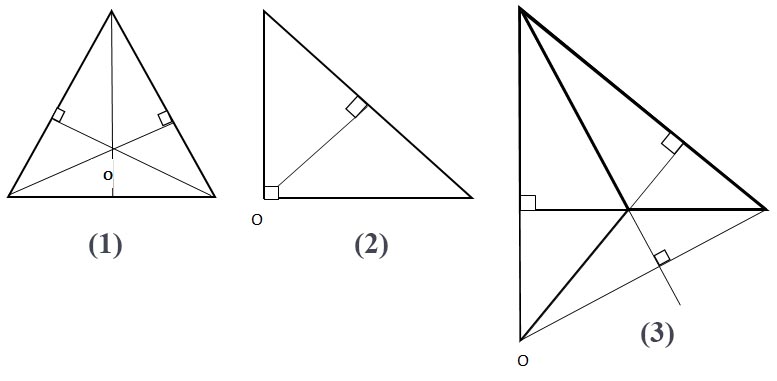
• У гострокутного трикутника точка перетину висот знаходиться у площині трикутника (Мал.1).
• У прямокутного трикутника точка перетину висот збігається з вершиною прямого кута (Мал.2).
• У тупокутного трикутника точка перетину висот знаходиться за площиною трикутника (Мал.3).
• У рівнобедреного трикутника медіана, бісектриса та висота, проведені до основи трикутника, збігаються.
• У рівностороннього трикутника всі три важливі лінії (висота, бісектриса і медіана) збігаються, і три важливі  точки
  (точки ортоцентра, центру тяжкості та центру вписаного та описаного кіл) знаходяться в одній точці перетину
  важливих ліній, тобто теж збігаються.

Формули знаходження висоти трикутника

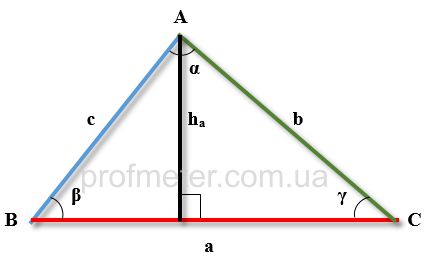
Малюнок наведено для полегшення сприйняття формул знаходження висоти трикутника.
Висота у формулах позначається літерою h, нижній індекс якої відповідає стороні, яку вона опущена.

Інші позначення:
a,b,c - довжини сторін трикутника
h_a - висота трикутника, проведена до сторони a з протилежного кута
h_b -висота, проведена до сторони b
h_c - висота, проведена до сторони c
R - радіус описаного кола
r - радіус вписаного кола

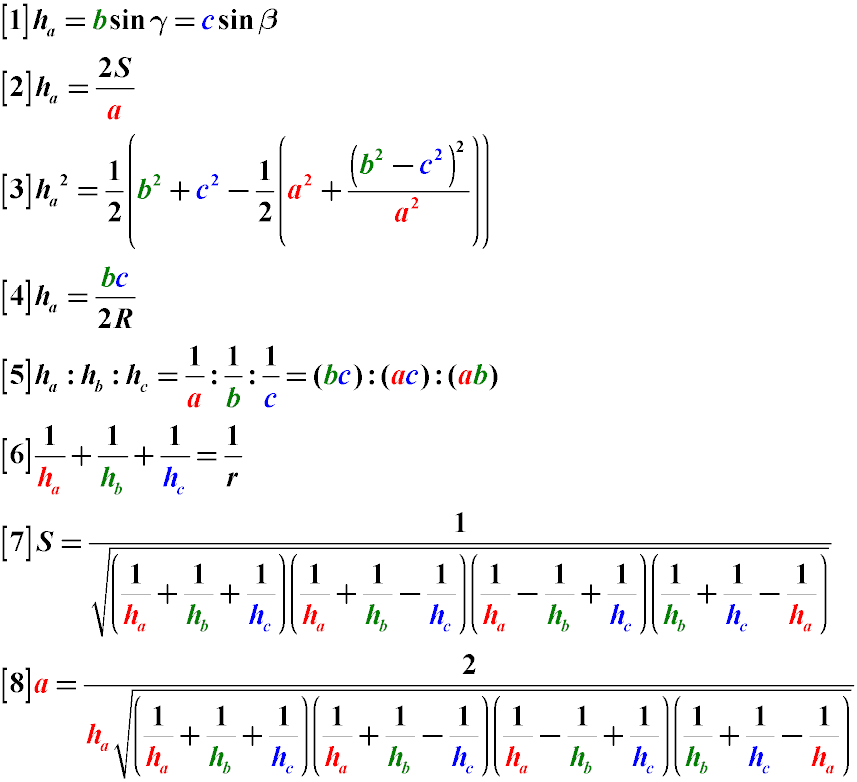
Пояснення до формул.

Висота трикутника дорівнює добутку довжини сторони, що прилягає до кута, з якої опущена ця висота на синус кута між цією стороною
та стороною, на яку така висота опущена (Формула 1)

Висота трикутника дорівнює частці від поділу подвоєної величини площі трикутника на довжину сторони, до якої опущена ця висота
(Формула 2)

Висота трикутника дорівнює частці від поділу твору сторін, що прилягають до кута, з якого опущена ця висота, на подвоєний радіус
описаного навколо нього кола (Формула 4).

Висоти сторін у трикутнику співвідносяться між собою в тій же пропорції, як співвідносяться між собою зворотні пропорції довжин сторін
цього ж трикутника, а також в тій же пропорції між собою відносяться твори пар сторін трикутника, які мають загальний кут (Формула 5).

Сума обернених значень висот трикутника дорівнює зворотному значенню радіусу вписаного в такий трикутник кола (Формула 6)

Площу трикутника можна знайти через довжини висот цього трикутника (Формула 7)

Довжину сторони трикутника, яку опущена висота, можна знайти через застосування формул 7 і 2.

Завдання щодо подібності трикутників. 

Рішення.

1. Визначимо довжину AB: Оскільки AD і BD є частинами гіпотенузи AB, ми можемо знайти AB, додавши AD і BD:

1. Використаємо теорему Піфагора: У прямокутному трикутнику ABC, де кут C = 90°, ми можемо застосувати теорему
   Піфагора для визначення довжини катетів AC і BC. Але спочатку нам потрібно знайти довжину CD.
2. Використаємо властивості подібності трикутників: Трикутники ADC і BDC є подібними до трикутника ABC, оскільки
   вони мають один спільний кут (кут C) і обидва мають прямий кут (кут D).

   Отже, ми можемо записати відношення сторін:
   CD / AD = BC / AB
   CD / BD = BC / AB

тобто:

DC²=AD*BD

DC²=9*16

DC=12 см

Завдання застосування теореми Пифагора.

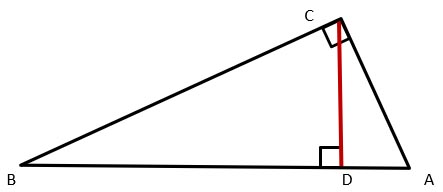
Трикутник ABC прямокутний. У цьому C-прямий кут. З нього проведена висота CD = 6см. Різниця відрізків BD-AD=5 см.

Знайти: Сторони трикутника ABC.



Рішення.

• Складемо систему рівнянь відповідно до теореми Піфагора

маємо п'ять невідомих, але, оскільки CD=6

36+BD²=BC²
36+AD²=AC²

маємо чотири невідомих, але,
оскільки BD-AD=5, то
BD = AD+5, тоді система рівнянь виглядає так:

36+(AD+5)²=BC²
36+AD²=AC²

маємо три невідомих.

36+(AD+5)²=BC²
36+AD²=AC²

Складемо перше та друге рівняння.
(якщо ви не знайомі з цим прийомом, знайте, що в системі рівнянь ці рівняння можна скласти між собою
і перейти до вирішення одного рівняння)
Оскільки ліва частина додається до лівої, а права частина до правої – рівність не буде порушено.
Отримаємо:

36+36+(AD+5)²+AD²=AC²+BC²

72+(AD+5)²+AD²=AC²+BC²

• Складемо рівняння для трикутника ABC
  

Глянувши на первісне креслення трикутника ABC, за теоремою Піфагора,
має виконуватись рівність:

AC²+BC²=AB²

Оскільки AB=BD+AD, рівняння буде виглядати таким чином: 

AC²+BC²=(AD+BD)²

Оскільки BD-AD=5, то BD = AD+5, тоді

AC²+BC²=(AD+AD+5)² 

• Тепер поглянемо на результати, отримані нами при вирішенні у першій та другій частині рішення.

72+(AD+5)²+AD²=AC²+BC²
AC²+BC²=(AD+AD+5)²

Вони мають загальну частину AC²+BC² . Таким чином, прирівнюємо їх один до одного.

72+(AD+5)²+AD²= (AD+AD+5)²

72+AD²+10AD+25+AD²=4AD²+20AD+25

-2AD²-10AD+72=0 

В отриманому квадратному рівнянні дискримінант дорівнює D=676, відповідно, коріння рівняння дорівнює:

х₁=-3,5

x₂=4 

Оскільки довжина відрізка може бути негативною, відкидаємо перший корінь.

AD=4

• Знайдемо довжини відрізків:

• Знайдемо довжину гіпотенузи AB:

• Знайдемо довжини катетів AC і BC: Використаємо теорему Піфагора для трикутника △ABC

По теореме Пифагора находим остальные стороны треугольника:

CD²+BD²=BC²

6²+9²=BC²

36+81=BC²

BC = √(117).

CD²+AD²=AC²

6²+4² = AC²

36+16=AC²

AC = √(52)