Для вирішення деяких завдань буде корисною таблиця тригонометричних тотожностей, яка дозволить набагато простіше здійснювати перетворення функцій:

Найпростіші тригонометричні тотожності

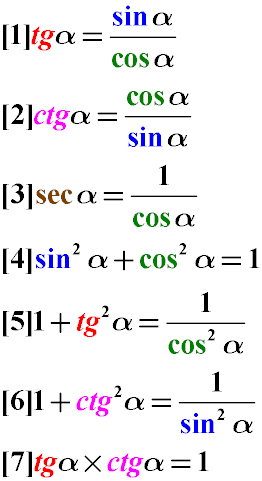
Частка від ділення синуса кута альфа на косинус того ж кута одно тангенсу цього кута (Формула 1). Див. Також доказ правильності перетворення найпростіших тригонометричних тотожностей.
Частка від ділення косинуса кута альфа на синус того ж кута одно котангенс цього ж кута (Формула 2)
Секанс кута дорівнює одиниці, поділеній на косинус цього ж самого кута (Формула 3)
Сума квадратів синуса і косинуса одного і того ж кута дорівнює одиниці (Формула 4). см. також доказ суми квадратів косинуса і синуса.
Сума одиниці і тангенса кута дорівнює відношенню одиниці до квадрату косинуса цього кута (Формула 5)
Одиниця плюс котангенс кута дорівнює частці від ділення одиниці на синус квадрат цього кута (Формула 6)
Твір тангенса на котангенс одного і того ж кута дорівнює одиниці (Формула 7).

Перетворення негативних кутів тригонометричних функцій (парність і непарність)

Для того, щоб позбутися від від'ємного значення градусної міри кута при обчисленні синуса, косинуса або тангенса, можна скористатися наступними тригонометричними перетвореннями (тотожністю), заснованими на принципах парності або непарності тригонометричних функцій.

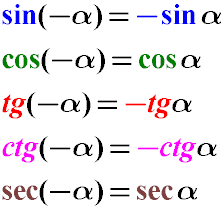
Як видно, косинус і секанс є парною функцією, синус, тангенс і котангенс - непарні функції.

Синус негативного кута дорівнює від'ємному значенню синусу цього ж самого позитивного кута (мінус синус альфа).
Косинус "мінус альфа" дасть теж саме значення, що і косинус кута альфа.
Тангенс мінус альфа дорівнює мінус тангенс альфа.

Формули приведення подвійного кута (синус, косинус, тангенс і котангенс подвійного кута)

Якщо необхідно розділити кут навпіл, або навпаки, перейти від подвійного кута до одинарного, можна скористатися наступними тригонометричними тотожністями: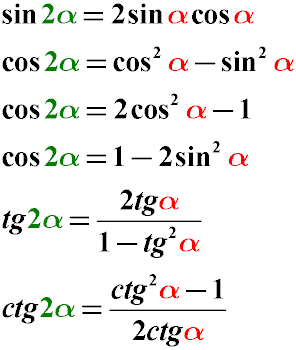 

Перетворення подвійного кута (синуса подвійного кута, косинуса подвійного кута і тангенса подвійного кута) в одинарний відбувається за такими правилами:

Синус подвійного кута дорівнює подвоєному добутку синуса на косинус одинарного кута

Косинус подвійного кута дорівнює різниці квадрата косинуса одинарного кута і квадрата синуса цього кута

Косинус подвійного кута дорівнює подвоєному квадрату косинуса одинарного кута мінус одиниця

Косинус подвійного кута дорівнює одиниці мінус подвійний синус квадрат одинарного кута

Тангенс подвійного кута дорівнює дробу, чисельник якого - подвоєний тангенс одинарного кута, а знаменник дорівнює одиниці мінус тангенс квадрат одинарного кута

Котангенс подвійного кута дорівнює дробу, чисельник якого - квадрат котангенс одинарного кута мінус одиниця, а знаменник дорівнює подвоєному котангенсу одинарного кута

Формули універсальної тригонометричної підстановки

Зазначені нижче формули перетворення можуть стати в нагоді, коли потрібно аргумент тригонометричної функції (sin α, cos α, tg α) розділити на два і привести вираз до значення половини кута. Зi значення α отримуємо α / 2.

Дані формули називаються формулами універсальної тригонометричної підстановки. Їх цінність полягає в тому, що тригонометричний вираз з їх допомогою зводиться до вираження тангенса половини кута, незалежно від того, які тригонометричні функції (sin cos tg ctg) були в вираженні спочатку. Після цього рівняння з тангенсом половини кута вирішити набагато простіше.

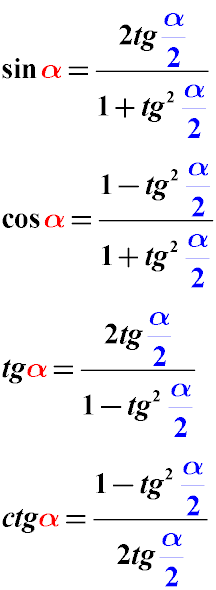
Тригонометричні тотожності перетворення половини кута

Зазначені нижче формули тригонометричного перетворення половинної величини кута до його цілого значення.
Значення аргументу тригонометричної функції α / 2 приводиться до значення аргументу тригонометричної функції α.

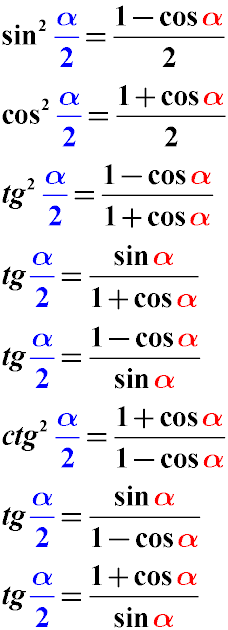
Тригонометричні формули додавання кутів

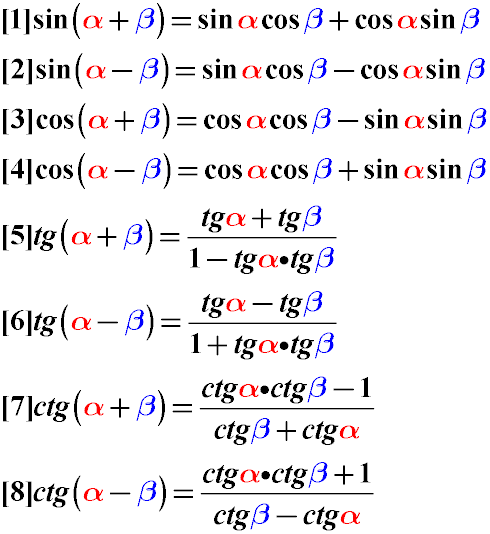
cos (α - β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α - β) = sin α · cos β - sin β · cos α 
cos (α + β) = cos α · cos β - sin α · sin β 

Тангенс і котангенс суми кутів альфа і бета можуть бути перетворені за такими правилами перетворення тригонометричних функцій:

Тангенс суми кутів дорівнює дробу, чисельник якого - сума тангенса першого і тангенса другого кута, а знаменник - одиниця мінус твір тангенса першого кута на тангенс другого кута.

Тангенс різниці кутів дорівнює дробу, чисельник якого дорівнює різниці тангенса зменшуваного кута і тангенса від'ємника кута, а знаменник - одиниці плюс твір тангенсов цих кутів.

Котангенс суми кутів дорівнює дробу, числівник якого дорівнює добутку котангенс цих кутів плюс одиниця, а знаменник дорівнює різниці котангенс другого кута і котангенс першого кута.

Котангенс різниці кутів дорівнює дробу, чисельник якого - твір котангенсів цих кутів мінус одиниця, а знаменник дорівнює сумі котангенсів цих кутів.

Дані тригонометричні тотожності зручно застосовувати, коли потрібно обчислити, наприклад, тангенс 105 градусів (tg 105). Якщо його представити як tg (45 + 60), то можна скористатися наведеними тотожними перетвореннями тангенса суми кутів, після чого просто підставити табличні значення тангенса 45 і тангенса 60 градусів.

Формули перетворення суми або різниці тригонометричних функцій

Вирази, що представляють собою суму виду sin α + sin β можна перетворити за допомогою наступних формул:

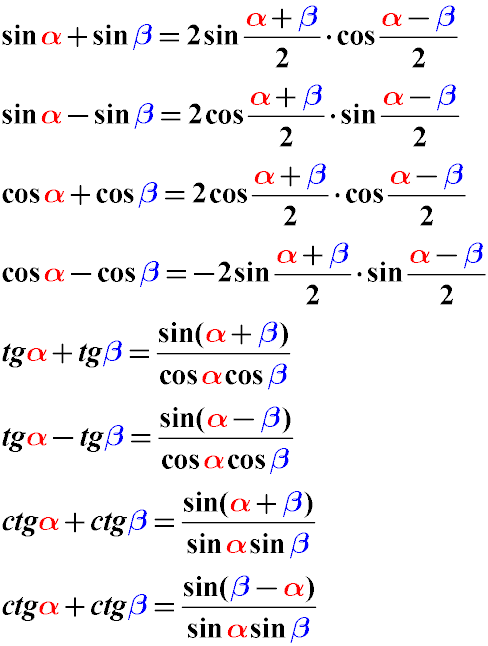
Формули потрійного кута - перетворення sin3α cos3α tg3α в sinα cosα tgα

Іноді необхідно перетворити потрійну величину кута так, щоб аргументом тригонометричної функції замість 3α став кут α.
В цьому випадку можна скористатися формулами (тотожністю) перетворення потрійного кута:

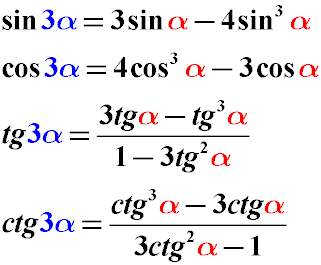
Формули перетворення добутку тригонометричних функцій

Якщо виникає необхідність перетворити твір синусів різних кутів косинусів різних кутів або навіть твори синуса на косинус, то можна скористатися наступними тригонометричними тотожностями:


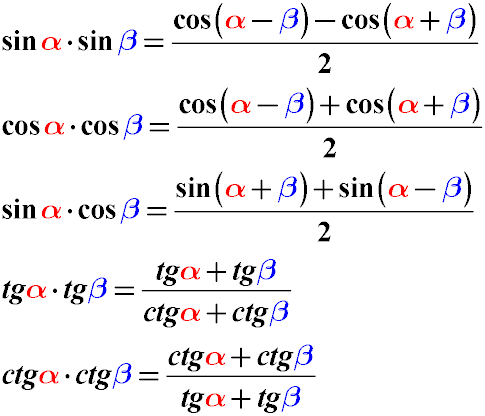
В цьому випадку твір функцій синуса, косинуса або тангенса різних кутів буде перетворено в суму або різницю.

Формули приведення тригонометричних функцій

Користуватися таблицею приведення потрібно в такий спосіб. У рядку вибираємо функцію, яка нас цікавить. У стовпці - кут. Наприклад, синус кута (α + 90) на перетині першого рядка та першого стовпчика з'ясовуємо, що sin (α + 90) = cos α.

См. також Повний список формул приведення тригонометричних функцій.

Кут	α + 90  α + π/2	α + 180  α + π	α + 270  α + 3π/2	90 - α  π/2- α	180 - α  π- α	270 - α  3π/2- α	360 - α  2π- α
sin	cos α	-sin α	-cos α	cos α	sin α	-cos α	-sin α
cos	-sin α	-cos α	sin α	sin α	-cos α	-sin α	cos α
tg	-ctg α	tg α	-ctg α	ctg α	-tg α	ctg α	-tg α
ctg	-tg α	ctg α	-tg α	tg α	-ctg α	tg α	-ctg α