|
|
Тангенс
Тригонометрична функція тангенс кута, позначається як tg. «Тангенс» дослівно перекладається з латинської як «що торкається».
Тангенс гострого кута прямокутного трикутника є відношення катета, що лежить проти цього кута, до другого катету.
Для візуального запам'ятовування: На малюнку внизу потрібні сторони трикутника позначені двосторонньою стрілкою.
"Синій" катет потрібно розділити на "червоний".
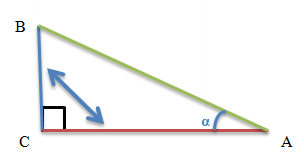
Простими словами, щоб обчислити тангенс кута в прямокутному трикутнику ми діємо наступним чином:
- Беремо довжину катета, протилежного гострого кута (α) - це катет BC, позначений синім кольором на малюнку
- Ділимо її на довжину другого катета (це катет AC, який позначений на малюнку червоним кольором)
- Отримане значення буде правильним і однаковим для заданої величини кута у будь-якому прямокутному трикутнику і
не буде залежати від розмірів трикутника
З цього випливає, що:
- Знаючи довжини катетів в прямокутному трикутнику, можна визначити значення тангенса кута, а потім, за допомогою функції arctg()
можна визначити величину цього кута
- Оскільки tg α завжди дорівнює tg α = BC / AC, то при відомій величині кута α і одного з катетів, завжди можна обчислити величину
другого катета
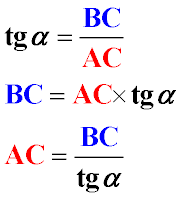
Описані вище співвідношення часто використовуються при вирішенні завдань. При цьому мається на увазі, що, використовуючи базову
властивість функції тангенса tg α = BC / AC (див. вище малюнок з позначеннями сторін), можливо легко знайти розміри трикутника або іншої
геометричної фігури. Однак, на практиці, саме це просте властивість тангенса і викликає труднощі при рішенні.
Тригонометрический круг тангенса. Тригонометричне коло тангенса
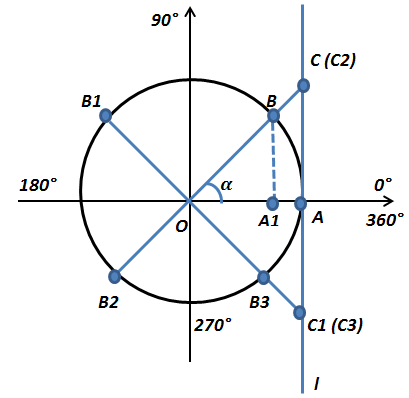
Лінія тангенсів - це дотична l до одиничного кола в точці А (1;0). За позитивний напрямок лінії тангенсів беруть напрямок знизу вгору.
З визначення тангенса кута (tg α = sin α / cos α) tg α = BA1 / OA1 = CA / OA = CA,так як ОА=1. Тобто, тангенс кута α - це величина відрізка
АС на лінії тангенсів. Інакше кажучи, тангенс кута - це величина відрізка дотичної, проведеної через точку А (кінець нерухомого радіуса),
від точки дотику А до перетину з продовженням рухомого радіуса ОВ.
Розглянемо зміна величини (відрізка АС) при русі рухомого радіуса OВ по колу і збільшенні кута.
Зауважимо, що значення збігаються у I і III квадрантах, у II і IV квадрантах:
Значення функції тангенсу кута (tg α)
Див. також тригонометрические значения тангенса часто встречающихся углов.
У таблиці нижче наведено відомості про те, яке значення функції тангенса (є воно позитивним чи негативним) для всіх від 0 до 360 градусів
(що відповідає значенням від 0 до 2π радіан). Для більш простого візуального запам'ятовування, там де функція тангенса приймає позитивні
значення, tg α позначено червоним кольором, а там, де негативні - синім.
|
Кут α
|
0
|
0° < α < 90°
|
90
|
90°<а<180°
|
180
|
180° < a < 270°
|
270
|
270°< а <360°
|
360
|
|
Значення функцiї tg α
|
0
|
0° < tg α < +∞
|
-
|
-∞ < tg α < 0
|
0
|
0° < tg α < +∞
|
-
|
-∞ < tg α < 0
|
0
|
Теорема косінусів. Приклад розв'язання задачі |
Описание курса
| Тригонометричне коло
|

