|
|
Примітка. Це частина уроку із завданнями з геометрії (розділ стереометрія). Якщо Вам необхідно вирішити задачу
з геометрії, якої тут немає - пишіть про це у форумі.
Завдання. Призма, вписана в циліндр
У циліндр вписано призму. Основою призми служить прямокутний трикутник, катет якого дорівнює 2а, а кут, що прилягає,
дорівнює 60 градусам. Діагональ більшої бічної грані призми складає з площиною її основи кут 45 градусів.
Знайдіть об'єм циліндра.

Рішення.
Об'єм циліндра знайдемо за формулою:
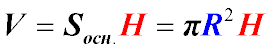
де:
R - радіус основи прямого циліндра,
h – висота.
Знайдемо основу циліндра. 1-й спосіб.
Основа циліндра одночасно є колом, описаним навколо прямокутного трикутника, що є основою призми.
Діаметр кола, описаного навколо прямокутного трикутника, лежить на його гіпотенузі. Тобто довжина гіпотенузи
дорівнює 2R.
Радіус кола, описаного навколо трикутника, знайдемо за формулою:
R = x / 2 sin α
де:
x - сторона трикутника
α - кут, що протилежить стороні а.
Протилежний кут знайдемо так. Оскільки трикутник прямокутний, то кут, що протилежить катету, буде дорівнювати
180-90-60 = 30 градусів. Таким чином, радіус описаного кола (він же радіус циліндра) дорівнює:
R = 2a / 2 sin 30 = 2a
Знайдемо основу циліндра. 2-й спосіб
У прямокутного трикутника гіпотенуза одночасно є діаметром описаного кола. Половина гіпотенузи дорівнюватиме
її радіусу.
Таким чином знайдемо гіпотенузу для прямокутного трикутника, знаючи кут та його катет через тригонометричну
функцію:
2R = 2a / cos 60 = 2a / 0.5 = 4a
R = 2a
Знайдемо висоту циліндра.
Діаметр описаного кола утворює з діагоналлю призми прямокутний трикутник, один катет якого є діаметром описаного
кола, другий - висотою циліндра та призми, а гіпотенуза є діагоналлю більшої сторони призми та одночасно циліндра.
Оскільки кут діагоналі з основою становить 45 градусів, то другий кут дорівнює 180 – 45 – 90 = 45 градусів.
Виходячи з того, що прямокутний трикутник рівнобедрений, то висота циліндра та призми дорівнює діаметру кола.
Таким чином:
V = пR2h
V = п * 4a2 * 4a
V = п16a3.
Відповідь: п16a3.
Завдання. У циліндр вписано правильну шестикутну призму.
У циліндр вписано правильну шестикутну призму. Знайти кут між діагоналлю її бічної грані та віссю циліндра,
якщо радіус основи дорівнює висоті циліндра.
Рішення.
Якщо радіус основи дорівнює висоті циліндра, діагональ бічної грані правильної шестикутної призми є прямокутним
трикутником, у якого один з катетів дорівнює висоті циліндра (r), а другий катет дорівнює стороні шестикутника,
вписаного в коло. Відповідно до властивостей шестикутника, вписаного в коло, його сторона дорівнює радіусу такого кола.
Тобто кожна бічна грань цієї вписаної призми – квадрат. Діагональ грані утворює з віссю циліндра, як і з бічним
ребром, однаковий кут 45 °, так як вісь циліндра і бічні ребра вписаної призми паралельні.
Циліндр |
Описание курса
| Осьовий переріз циліндра
|

