|
|
Елліпс - геометричне місце точок X Евклідової площини, для яких сума відстаней від двох даних точок F1 і F2 (називаються фокусами)
постійна, тобто | F1X | + | F2X | = 2a.
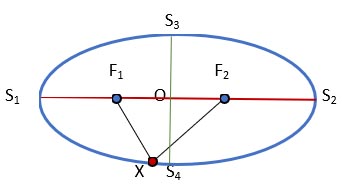
Загальноприйняті позначення для формул, що описують властивості еліпса, вказані на малюнку:
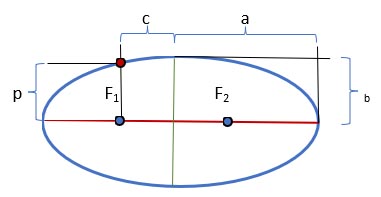
- Велика вісь еліпса - це відрізок, що проходить через фокуси еліпса, обмежений еліпсом.
Довжина великої осі дорівнює 2a.
- Мала вісь еліпса - це відрізок, перпендикулярний до великої осі еліпса, що проходить через її центр, і обмежений самим еліпсом.
Довжина малої осі дорівнює 2b.
- Велика та мала півосі еліпса (a і b) – це відрізки, проведені з центру еліпса до вершин на великій та малій осях.
- Фокальна відстань (c) – це відстань від центру еліпса до його фокусу.
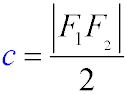
- Ексцентриситет (e) – це співвідношення фокальної відстані та великої півосі еліпса. Він однозначно характеризує величину
"деформації" еліпса по відношенню до кола і знаходиться в інтервалі [0, 1). Ближче до нуля – ближче до кола.
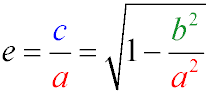
- Коефіцієнт стиснення еліпса - це відношення довжин малої та великої півосей.
Якщо говорять про стиснення еліпса, то мають на увазі значення (1-k)
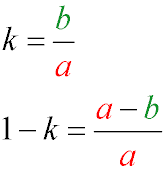
Для кола коефіцієнт стиску дорівнює одиниці, стиснення - нулю.
- Коефіцієнт стиснення та ексцентриситет еліпса пов'язані співвідношенням
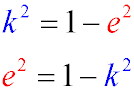
- Діаметром еліпса називається будь-яка хорда, що проходить через його центр.
- Пару діаметрів, що мають наступну властивість, називають сполученими якщо:
середини всіх хорд, паралельних одному з них, розташовані на другому діаметрі.
Аналогічно, середини хорд, паралельних другому діаметру, лежать першому.
- Радіус еліпса в цій точці це відрізок, що з'єднує центр еліпса з точкою, а також його довжина, яка обчислюється за формулою
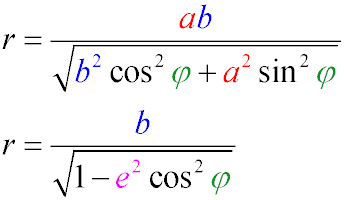
де φ - кут між радіусом і великою піввіссю.
- Фокальний параметр - це половина довжини хорди, яка проходить через фокус еліпса і перпендикулярна до його великої осі.
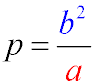
Канонічне рівняння еліпса
Для будь-якого еліпса можна знайти декартову систему координат таку, що еліпс описуватиметься рівнянням (канонічне рівняння еліпса):
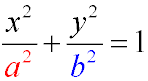
Канонічний рівняння еліпса описує еліпс з центром на початку координат, осі якого збігаються з осями координат.
Для певності припустимо, що 0 < b ≤ a. У цьому випадку величини a і b - відповідно, велика і мала півосі еліпса.
Знаючи півосі еліпса можна обчислити його фокальну відстань та ексцентриситет:
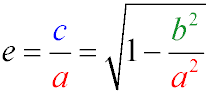
Координати фокусів еліпса в цьому випадку будуть (ae; 0), і (-ae; 0)
Еліпс має дві директриси, рівняння яких можна записати як
х = a / ε і х = - a / ε
Рівняння діаметра еліпса, сполученого хордам з кутовим коефіцієнтом k:
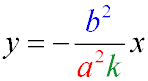
Рівняння дотичних еліпса, що проходять через точку (x1y1)
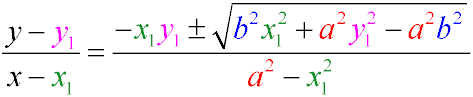
Рівняння дотичних еліпса, що мають даний кутовий коефіцієнт
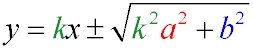
Рівняння нормалі еліпса у точці (x1y1)
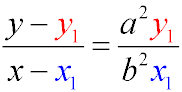
Приклади розв'язання задач
Завдання.
Знайдіть ексцентриситет еліпса
x2 / 8 + y2 / 6 = 1
Рішення.
За формулою знаходження ексцентриситету еліпса (див. вище)
ε = √(64 - 36) / 8
ε = √28 / 8 = 2√7 / 8 = √7 / 4 ≈ 0,66 ≈ 2/3
Хорда |
Описание курса
| Трикутник
|

