АКСІОМА 3. ВЛАСТИВОСТІ ВИМІРЮВАННЯ ВІДРІЗКІВ
Кожен відрізок має певну довжину, більшу нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
Дане твердження є аксіомою, тобто воно спочатку приймається як вірне і доказу не підлягає.
Коментар
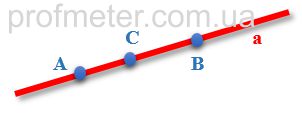
Візьмемо пряму a і позначимо на ній точки A і B, які утворюють відрізок AB, що належить цій прямій. Оскільки точки A і B не збігаються, то довжина відрізка AB більше нуля.
Якщо на відрізку взяти будь-яку точку, крім точок початку і кінця відрізка, то відрізок розбивається цією точкою на два відрізки і його довжина дорівнює сумі довжин цих відрізків.
Між точками A і B позначимо точку C, яка розіб'є відрізок AB на дві частини - AC і CB.
Довжина відрізка АВ дорівнює сумі довжин відрізків АС і СВ:
АВ = АС + СВ
В цьому і полягає твердження аксіоми.
Довжина кожного з отриманих відрізків дорівнює різниці довжин цілого відрізка (АВ) і його другої частини (СВ або АС).
АС=АВ-СВ і СВ=АВ-АС
На підставі затвердження цієї аксіоми побудовано доказ більшості теорем планіметрії і стереометрії.

